Gray:
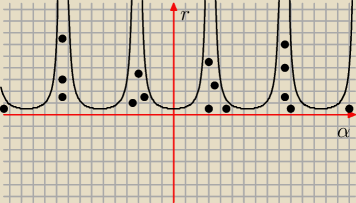
Można to wyznaczyć w układzie Oαr (zamiast Oxy)
z=r(cosα+isinα), więc
|z|+Re(z) = r + rcosα <1 ⇔ r(1+cosα)<1, co dla α≠π+kπ daje:
Dla α=π+kπ, r + rcosα = 0 więc nierówność jest spełniona.
Rozwiązaniem będzie więc fragment płaszczyzny zawarty w górnej półpłaszczyźnie i ograniczony od
| | 1 | |
góry wykresem funkcji r= |
| dla α≠π+kπ. |
| | 1+cosα | |
Na rysunku masz wykres tej właśnie funkcji (to co zakropkowałem, to Twój obszar).