TRYGONOMETRIA Blue: Wyznacz wszystkie wartości parametru m, dla których równanie cos²x−cosx+m=0 ma co najmniej jedno rozwiązanie.

	1
Robię tak cosx=t , liczę deltę i ona musi być większa lub równa zero czyli m≤		, ale muszę
	4

jeszcze wziąć pod uwagę to, że cosx ∊<−1,1> Jak to zrobić?

Kacper: Równanie t²−t+m=0 ma mieć co najmniej jedno rozwiązanie w przedziale <−1,1>.

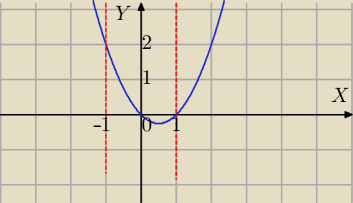
Mila: Przekształcam równanie : cos²x−cosx=−m cosx=t i t∊<−1,1> f(t)=t²−t wartość najmniejsza i największa f(t) w przedziale <−1,1>

	1
tw=		∊<−1,1> w takim razie najmniejsza wartość f(t) jest dla tw
	2

	1		1
f(		)=−
	2		4

Wartości największej szukam na końcach przedziału f(−1)=1+1=2 f(1)=0 2− wartość największa f(t) w przedziale <−1,1>

	1
−		≤−m≤2 rozwiąż.
	4

Warto naszkicować wykres f(t).

Kacper: Podaj odpowiedź jaką masz

Kacper: Mila ubiegła mnie w identycznym rozwiązaniu Łatwiejsze niż standardowe liczenie warunków dla równania kwadratowego.

Koko:

	(−b+√Δ)		(−b−√Δ)
t∊<−1,1> i t=		lub t=
	2a		2a

Z tego wyliczamy deltę, wychodzi, że po podstawieniu a i b mamy: Δ=(2*|t|−1)² Gdzie |t| <= 1 Czyli mamy, że 1−4m=4t²−4|t|+1 Mamy, że m=|t|−t². To już umiesz rozwiązać ?

Koko: Jeśli się nie pomyliłem w przekształceniach to powinno dobrze wyjść.

Blue:

	1
w odpowiedziach mam m∊<−2,		>
	4

Blue: No czyli wyjdzie to samo, bo tam jest jeszcze minus Dziękuję Mila