Wykaż, że |AC|^2 + |BD|^2 =4R^2
piotr: W okręgu o promieniu R poprowadzono dwie prostopadłe cięciwy AB i CD .Wykaż, że |AC|2 + |BD|2
=4R2
16 lis 19:31
Eta:
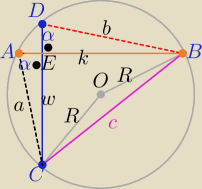
|AC|=a , |DB|=b , |EB|=k, |EC|=w , |BC|=c
|∡CAB|=|∡CDB|=α −−− kąty wpisane oparte na tym samym łukuCB
| | c | |
z tw. sinusów w trójkącie BDC : |
| =2R ⇒c=2R*sinα |
| | sinα | |
oraz w trójkątach prostokątnych AEC i DEB:
w=a*sinα i k=b*sinα
z tw. Pitagorasa w ΔCEB: w
2+k
2=c
2
to:
a
2sin
2α+b
2*sin
2α= 4R
2*sin
2α / : sin
2α≠0
a
2+b
2= 4R
2 ⇔
|AC|2+|BD|2=4R2
c.n.w.
16 lis 20:39
 |AC|=a , |DB|=b , |EB|=k, |EC|=w , |BC|=c
|∡CAB|=|∡CDB|=α −−− kąty wpisane oparte na tym samym łukuCB
|AC|=a , |DB|=b , |EB|=k, |EC|=w , |BC|=c
|∡CAB|=|∡CDB|=α −−− kąty wpisane oparte na tym samym łukuCB