Michał: W trójkącie ABC, w którym kąt A jest prosty, kreślimy koło styczne do boków BC i AC,
mające środek na boku AB. Koło to przecina bok AB w punkcie M i jest styczne do
przeciwprostokątnej w punkcie D. Wykaż, że jeżeli na przedłużeniu boku AC odłożymy CE,
|CE| = |AC| , to punkty M, E, D leżą na jednej prostej.
18 paź 15:07
Dami:
Widze ciekawe zadanie, no ale niestety nie umiem rozwiązać...
18 paź 20:59
Lukasz:
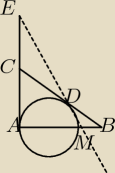
ABCEDMAMDCE, Tak wygląda rysunek. Dalej |CA|=|CD|, kątADB=90st
Dalej można poprowadzić promienie okręgu do punktu D i tam wychodzą kąty proste. Czy ma koś
pomysł jak dalej powinno isę zrobić to zadanie? Wydaje mi się, iż kąt ADE też pwoinien być
prosty. Tylko musimy wczesniej połączyć punkty A i D.
26 wrz 17:55
Vax: Oznacz sobie środek tego okręgu jako O (Zauważ, że jest to punkt przecięcia dwusiecznej <ACB i
boku |AB|) i pokaż, że CO || EM oraz CO || ED, stąd będzie wynikała dana współliniowość.
26 wrz 18:39
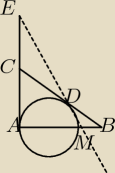 ABCEDMAMDCE, Tak wygląda rysunek. Dalej |CA|=|CD|, kątADB=90st
Dalej można poprowadzić promienie okręgu do punktu D i tam wychodzą kąty proste. Czy ma koś
pomysł jak dalej powinno isę zrobić to zadanie? Wydaje mi się, iż kąt ADE też pwoinien być
prosty. Tylko musimy wczesniej połączyć punkty A i D.
ABCEDMAMDCE, Tak wygląda rysunek. Dalej |CA|=|CD|, kątADB=90st
Dalej można poprowadzić promienie okręgu do punktu D i tam wychodzą kąty proste. Czy ma koś
pomysł jak dalej powinno isę zrobić to zadanie? Wydaje mi się, iż kąt ADE też pwoinien być
prosty. Tylko musimy wczesniej połączyć punkty A i D.