Geometria Blue: W trójkącie prostokątnym dwusieczna kąta prostego dzieli przeciwprostokątną na odcinki, których stosunek długości, których stosunek wynosi 2:1. W jakim stosunku wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną

Blue: Czekajcie , chyba coś mi wychodzi, nie podpowiadajcie

Blue: wyszło mi 1:4 − jest ok Niepotrzebnie wrzucałam ^^

Eta: ok

Blue: Ale z tym chyba będę potrzebowała pomocy: W trójkącie ABC poprowadzono środkową CK, a następnie poprowadzono dwusieczne kątów AKC i BKC, które przecinają boki AC i BC odpowiednio w punktach P i Q . Wykaż, że trójkąty ABC i PQC są podobne

Blue: Czekam

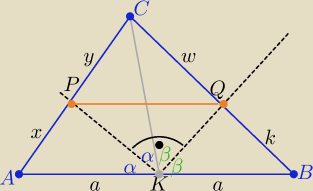
Eta: 1/ sposób z własności dwusiecznych:

a		|CK|		a		|CK|		ay		aw
	=		i		=		⇒ |CK|=		=
x		y		k		w		x		k

	y		w
to :		=
	x		k

boki trójkątów ABC i PQC są proporcjonalne i mają wspólny kąt między nimi γ z cechy (b,k,b) są podobne 2 sposób Sama............ zauważ ,że 2α+2β=180^o ⇒ α+β= 90^o ..................

Blue: dzięki Eta

Eta: Zapomniałam na rys zaznaczyć : γ= |∡ACB|

Blue: Domyśliłam się