wyznacz orgami: wyznacz najmniejszą i największą wartośc funkcji f (x) = 2 (x − 1)² − 3 w przedziale <− 2; 2> bardzo proszę o rozwiązanie i wytłumaczenie krok po kroku dla mnie jest to czarana magia, z góry dziękuję

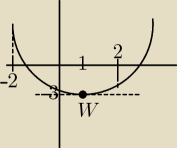
ula: masz podany wzór paraboli w postaci kanonicznej, z niego można łatwo określić W (wierzchołek) y=a(x−p)²+q → W(p;q) porównaj swój wzór i kanoniczny i z niego wynika że W(1;−3) pilnuj znaków bo można łatwo się pomylić można wyliczyć też miejsca zerowe, ale nie koniecznie − będzie dokladniejszy rysunek 0=2(x−1)²−3 minimum (czyli y jest najmniejsze) jest dla wierzchołka (wartość y w wierzchołku) czyli −3 teraz obliczamy max podsraw pod x wartości −2 , 2, sprawdź gdzie y będzie największy y=2(−2−1)²−3 y=2(2−1)²−3 y=−1 y=15 największa wartość to 15

orgami: dzięki bardzo , dużo mi to pomogło ale nie bardzo wiem skąd wzięły ci się te wyniki y = 15 i y = −1 ? jakbyś mogła mi to napisać krok po kroku. jak nie byłby problem to mogłabyś mi jeszcze wyliczyć to miejsce zerowe, będe bardzo wdzieczna dla mnie to czarna magia, ale dzieki twojemu rozwiązaniu zaczynam coś rozumiec

pati: f (x) = 2 (x − 1)² − 3 <− 2; 2> Najpierw zamieniamy postac kanoniczna funkcji na postac ogolna czyli podnosimy nawias do potegi i wymnazamy f (x) = 2 (x − 1)² − 3 f (x) = 2 (x² − 2x +1) − 3 f (x) = 2x² −4x +2− 3 f (x) = 2x² − 4x − 1 Będziemy musieli policzyć 3 wartości − współrzędną y wierzchołka paraboli (o ile czyli wartość x należy do przedziału!) oraz wartości funkcji z krańców podanego przedziału, które to policzymy na poczatku: f( − 2) = 2 (−2)² − 4 *(−2) −1 = 2 *4 + 8 − 3 = 8+5 = 13 f(2) =2 * (2 )² − 4 * 2− 3 = 2 * 4 − 8 − 3= 8 − 8 − 3= −3 Współrzędna x wierzchołka (czyli p): p={−b}\{2a} = −{−4}\{4} = 4\4=1 x=1 należy do przedziału <−2, 2> (gdyby tak nie było, wierzchołek leżałby poza rozpatrywanym przedziałem, wówczas już nas nie interesuje). Ponieważ a>0 (a = 2), funkcja osiąga w punkcie wierzchołka minimum, o czym zaraz się przekonamy. Obliczamy y wierzchołka (czyli q), korzystając z wartości p=1. f(1 ) = 2 * 1² − 4 *1 − 3=2 − 4 − 3= −5 Uzyskaliśmy więc: wartość −13 dla x=− 2, wartość − 3 dla x=2 oraz wartość − 5 dla x=1. Jak nie trudno się domyśleć, największa wartość będzie szukanym maksimum, najmniejsza − minimum. Podsumowując, funkcja osiąga minimum dla x= −2 oraz maksimum dla x=2 (biorąc pod uwagę przedzialał <−2, 2>). Mam nadzieję że dobrze skonsultuj to z kimś Powodzenia

pati: f (x) = 2 (x − 1)² − 3 <− 2; 2> Najpierw zamieniamy postac kanoniczna funkcji na postac ogolna czyli podnosimy nawias do potegi i wymnazamy f (x) = 2 (x − 1)² − 3 f (x) = 2 (x² − 2x +1) − 3 f (x) = 2x² −4x +2− 3 f (x) = 2x² − 4x − 1 Będziemy musieli policzyć 3 wartości − współrzędną y wierzchołka paraboli (o ile czyli wartość x należy do przedziału!) oraz wartości funkcji z krańców podanego przedziału, które to policzymy na poczatku: f( − 2) = 2 (−2)² − 4 *(−2) −1 = 2 *4 + 8 − 3 = 8+5 = 13 f(2) =2 * (2 )² − 4 * 2− 3 = 2 * 4 − 8 − 3= 8 − 8 − 3= −3 Współrzędna x wierzchołka (czyli p): p={−b}\{2a} = −{−4}\{4} = 4\4=1 x=1 należy do przedziału <−2, 2> (gdyby tak nie było, wierzchołek leżałby poza rozpatrywanym przedziałem, wówczas już nas nie interesuje). Ponieważ a>0 (a = 2), funkcja osiąga w punkcie wierzchołka minimum, o czym zaraz się przekonamy. Obliczamy y wierzchołka (czyli q), korzystając z wartości p=1. f(1 ) = 2 * 1² − 4 *1 − 3=2 − 4 − 3= −5 Uzyskaliśmy więc: wartość −13 dla x=− 2, wartość − 3 dla x=2 oraz wartość − 5 dla x=1. Jak nie trudno się domyśleć, największa wartość będzie szukanym maksimum, najmniejsza − minimum. Podsumowując, funkcja osiąga minimum dla x= −2 oraz maksimum dla x=2 (biorąc pod uwagę przedzialał <−2, 2>). Mam nadzieję że dobrze skonsultuj to z kimś Powodzenia

Aurelia: Tu jest błąd f( − 2) = 2 (−2)2 − 4 *(−2) −1 = 2 *4 + 8 − 1 = 8+5 = 13 f(2) =2 * (2 )2 − 4 * 2− 3 = 2 * 4 − 8 − 3= 8 − 8 − 3= −3 Powinno być tak : f( − 2) = 2 (−2)2 − 4 *(−2) −1 = 2 *4 + 8 − 1 = 8+8−1 = 15 f(2) =2 * (2 )2 − 4 * 2− 3 = 2 * 4 − 8 − 3= 8 − 8 − 1= −1

Aurelia: Na końcu wychodzi ymin −1 dla 2 y max 15 dla −2

Annaaa: jak rozwiązać ? f(x)= −x2−4x−2 w przedziale x należy <−1;2>

Kuba: Wyznacz wartość najmniejszą i wartość największą funkcji f(x)=2x²−5x+3 w przedziale (−1;2)

Kaja: przedział powinien być chyba domknięty. policz f(−1), f(2) i współrzędną x_w wierzchołka z odpowiedniego wzoru i jesli ten x_w należy do przedziału <−1;2>, to policz f(x_w). z wyliczonych wartości wybierz najmniejsza i najwiekszą