funkcja wykładnicza maturzysta: Znaleźć liczbę całkowitą p dla której równanie 3^2x−4*3^x+p=0 ma dwa pierwiastki całkowite

pigor: ... , widzę to tak :warunki zadania spełnia układ nierówności Δ=16−4p>0 (warunek istnienia dwóch oraz c=p∊C>0 całkowitych dodatnich pierwiastków 3^x>0, czyli ⇔ 0< p< 4, skąd p=3 − szukana liczba p , a wtedy faktycznie 3^x=3 v 3^x=1 ⇔ x∊{0,1} − 2 pierwiastki całkowite.

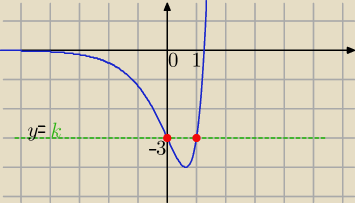Eta: f(x)= 3^x(3^x−4) i y= k= −p k= −3 ⇒ p=3