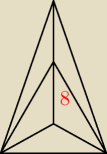
 Dany jest ostroslup prawidłowy trójkątny. Ściana boczna tworzy z plaszczyzną podstawy kąt 60•
Wysokość ostroślupa wynosi 6. Oblicz objętość tej bryły.
Dany jest ostroslup prawidłowy trójkątny. Ściana boczna tworzy z plaszczyzną podstawy kąt 60•
Wysokość ostroślupa wynosi 6. Oblicz objętość tej bryły.

 Dany jest ostroslup prawidłowy trójkątny. Ściana boczna tworzy z plaszczyzną podstawy kąt 60•
Wysokość ostroślupa wynosi 6. Oblicz objętość tej bryły.
Dany jest ostroslup prawidłowy trójkątny. Ściana boczna tworzy z plaszczyzną podstawy kąt 60•
Wysokość ostroślupa wynosi 6. Oblicz objętość tej bryły.

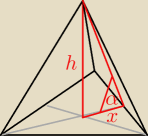 α = 60o
h = 6
więc
α = 60o
h = 6
więc
| h | |
= tg α = tg 60o = √3 | |
| x |
| 6 | |
= √3 ⇒ 6 = x √3 | |
| x |
| 6 | ||
x = | = 2√3 | |
| √3 |
| √3 | ||
hp = a | ||
| 2 |
| √3 | ||
6 √3 = a | ||
| 2 |
| 1 | 1 | a2 √3 | ||||
V = | Pp *h = | *h = | ||||
| 3 | 3 | 4 |
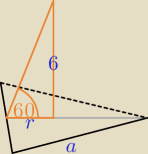 można i tak:
można i tak:
| 1 | ||
r = | a√3 i z własności trójkąta prostokątnego o kącie ostrym 60o: r√3 = 6 | |
| 6 |
| 1 | 1 | ||
a√3*√3 = 6 /2 ⇒ | a2 = 36 | ||
| 6 | 4 |
| 1 | 1 | 1 | ||||
Objętość V = | * | a2√3*6 = | *36*√3*6 = ... | |||
| 3 | 4 | 3 |
