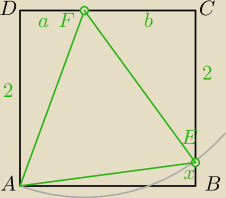
Trójkąt wpisany w kwadrat - udowodnienie. humbak: W kwadrat ABCD o boku 2 wpisano trójkąt równoramienny AEF tak, że wierzchołek E leży na boku BC, a wierzchołek F− na boku CD oraz |AF|=|EF|. Niech x=|BE|. Wykaż, że funkcja

	1
P(x)=2−		x(x−2)2 opisuje pole trójkąta AEF dla x∊<0,2>.
	8

Będę wdzięczny za wszelkie wskazówki.

Tadeusz:

Tadeusz: Policz pole Δ_AEF jako różnicę pola kwadratu i pól Δ_ADF, Δ_CEF i Δ_ABE

:): Mógłby ktoś to rozwiązać, albo chociaż napisać jakieś wyjściowe równanie, bo nie moge tych pól obliczyć...

kreskaNWJ: |CE|=2−x |CF|=2−a Skorzystaj teraz z Pitagorasa i masz a²+4=(2−a)²+(2−x)² (bo |AF|=|EF|) Wyliczasz sobie a w zależności od x no i możesz już obliczyć wszystkie pola od x. Dalej już powinieneś sobie poradzić

	−x2+4x+4
a powinno wyjść
	4