 Mam problem z jedynm zadaniem.
Nie mogłem narysować diagramu, więc wrzucam poniżej:
http://zapodaj.net/ab8aa04f0c055.png.html
Treść zad:
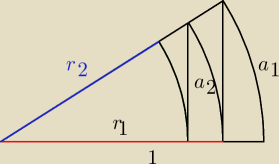
Na rysunku widoczny jest wycinek koła (AOB) o promieniu 1 i środku O, gdzie długość łuku AOB =
θ. Linie (AB1), (A1B2), (A2B3) są prostopadłe do OB. A1B1, A2B2 są łukami kół o
środku O.
Oblicz sumę (do nieskończoności) długości łuków:
AB + A1B1 + A2B2 + A3B3 + ...
Mam problem z jedynm zadaniem.
Nie mogłem narysować diagramu, więc wrzucam poniżej:
http://zapodaj.net/ab8aa04f0c055.png.html
Treść zad:
Na rysunku widoczny jest wycinek koła (AOB) o promieniu 1 i środku O, gdzie długość łuku AOB =
θ. Linie (AB1), (A1B2), (A2B3) są prostopadłe do OB. A1B1, A2B2 są łukami kół o
środku O.
Oblicz sumę (do nieskończoności) długości łuków:
AB + A1B1 + A2B2 + A3B3 + ...
| θ | θ | |||
dł. luku to | •2πr= | πr | ||
| 360 | 180 |
| θ | ||
zauważ że c= | π jest stałe , zatem | |
| 180 |

 α∊(0,90)
α∊(0,90)
| α | ||
dł łuku | *2πr | |
| 360 |
 pisząc oznaczenia odcinków chodzi mi o łuki.
pisząc oznaczenia odcinków chodzi mi o łuki.
| α | ||
|AB|= | *2π | |
| 360 |
| r1 | ||
cosα= | ⇒r1=cosα | |
| 1 |
| r2 | ||
cosα= | ⇒ r2=r1cosα | |
| r1 |


 czyli długość łuku AnBn=(α/360)*2πrn=(α/360)cosnα
czyli długość łuku AnBn=(α/360)*2πrn=(α/360)cosnα
| α | ||
S∞= | ||
| 1−cos(α) |