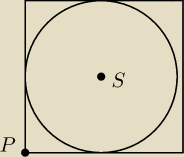
geometria analityczna olkaq: Hej, pomoże ktoś w takim dość ciekawym zadaniu z geometrii analitycznej: Wykaż , że e P=(5,−4) może być wierzchołkiem kwadratu opisanego na okręgu x² + y² −4x + 10y + 24 = 0 Równanie okręgu: (x − 2)² + (y + 5)² = 5 ⇒ Środek okręgu: (2,−5) Promień = √5

Janek191: Oblicz I P S I Powinno być równe √2*r = √2*√5 = √10

olkaq: I to tyle wystarczy Nic więcej i to będzie cały dowód ?

Ditka: 2*√5−bok kwadratu połowa jego przekątnej (odległość wierzchołka kwadratu od środka okręgu)− 2√5√2/2=√5√2=√10 |PS|=√(2−5)²+(−5+4)²=√10 −może być wierzchołkiem

olkaq: ok. Coś zrozumiałam Dzięki wielkie for you