Sinusoida i cosinusoida 155178: Podaj wszystkie argumenty dla których sinx=cosx x∊<−5π;4π). Jak to obliczyć ? Bo narysowałem rysunek, mam punkty przecięcia się, ale ciężko jest je wyliczyć bardzo. Pomógłby ktoś ?

Kacper: Jeśli cosx≠0 to możemy podzielić przez cosx

PW: Kacper ma rację, ale dlaczego piszesz "ciężko jest je wyliczyć bardzo". Nie wiesz, że

	√2
sin45° = cos45° (=		) ?
	2

155178: Ale to jest wartość, a nie argument.

155178: Wyszło mi, że dla x∊{−4³₄π;−3³₄π;−2³₄π;−1³₄π;−³₄π;^π₄;1¹₄π; 2¹₄π;3¹₄π} Dla 2sinx=2cosx argumenty przecięcia się będą takie same ? Przecież zmienią się tylko wartości obu funkcji, ale argumenty przecięcia się pozostaną bez zmian ? @PW JUŻ ROZUMIEM. FAKTYCZNIE ! ZAPOMNIAŁEM O TYM KOMPLETNIE BO SKUPIŁEM SIĘ NA RYSUNKU I NIE MOGŁEM TRAFIĆ W PUNKT, ale wywnioskowałem z rysunku, że ^π₄ w okresie π.

155178: @ODSWIEZAM

155178: @MAŁPKA

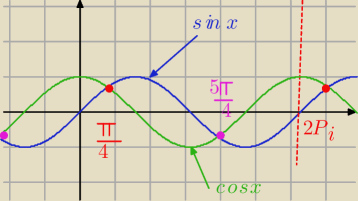
Mila: Z wykresu , albo : tg(x)=1

	π
x=		+kπ
	4

i po kolei k=0,−1,1, aby rozw. ∊<−5π,4π> Dobrze podałeś rozwiązania.

155178: A jak mam sin2x=cos2x to co z argumentami przecięcia się dzieje ? punkty maleją dwukrotnie tak samo jak wykres się "zwęża" ? Mógłbyś podać mi punkty przecięcia w tej dziedzinie dla sin2x=cos2x, bo nie rozumiem tego do końca ;\

Mila: Po kolacji.

Kacper: Mila smacznego

	π		π
155178 jeśli sinx=cosx dla		, to sin2x=cos2x jest równe dla
	4		8

Mila: Dziękuję Kacper

155178: A co się dzieje z okresem tych punktów, nadal powtarzają się co π czy teraz co ^π₂

Mila: tg(2x)=1

	π
2x=		+kπ /:2
	4

	π		π
x=		+k*
	8		2