płaszczyzna zespolona floridaa: Naszkicować zbiór{z∊C: |z3|≤8 , 0≤ arg(z3)≤π/4} szczególnie w tym zadaniu chodzi mi o to jak przyjmować wartości k w wzorze na argzn= n*argz + 2kπ

Gray: arg(z³) = 3argz + 2kπ, czyli

	2π		π		2π
0≤3argz + 2kπ≤π/4 ⇔		k≤ argz ≤		+		k
	3		12		3

Teraz dobierasz takie k, aby te obszary mieściły się w okresie funkcji arg, tj. [0,2π), aby się nie powtarzało. Wychodzi k=0,1,2. Dla k=3 masz to samo co dla k=0...

floridaa: a jeszcze jedno pytanie.. czemu po przeniesieniu 2kπ/3 na lewa i prawa strone dodaje sie ta wartość do poprzednich ( tak jak w przykładzie wyżej π/12 + 2kπ/3 a nie −) a nie odejmuje ? od czego to zależy?

J :

	2π		2π
k jest liczbą całkowitą , więc: −		=		*(−1) [ k = −1 ]
	3		3

floridaa: w pewnych przykładach spotkałam sie że odejmuje się ta wartość a nie dodaje dlatego nie rozumiem tego nadal czemu akurat w tym przykladzie do obu stron dodajemy 2kπ/3

Gray: Możesz odejmować. Ale wtedy przyjmiesz k=0,−1,−2. Skoro k jest dowolną liczbą całkowitą to nie ma znaczenia czy napisze k czy −k.

J : .... bo tutaj znak wyrażnia zależy od znaku k ( dla k > 0 znak + , dla k < 0 znak −)

2π		2π		2π		2π
	*k =		dla k = 1 , ale		*k = −		dla k = − 1 ..
3		3		3		3

floridaa: ok dziękuje a jeszcze mam przykład taki : obliczyć w (i) a nastepnie znaleźć wszystkie pierwiastki wielomianu w(z)=z⁴−z³+2z²−z+1... i nie mam pojęcia jak zabrac sie za obliczenie tego w(i)

Gray: i² = −1, zatem w(i) = i⁴ − i³ +2i² −i+1 = 1 + i −2 −i+1 = 0. Skoro i jest pierwiastkiem tego wielomianu to −i też. Oznacza to, że wielomian w dzieli się przez (z−i)(z+i) = z²+1. Dzieląc w przez ten wielomian otrzymasz wielomian kwadratowy − jego zera obliczysz bez trudu przy pomocy Δ.

floridaa: kurcze nadal nie moge narysowac tych zespolonych z przykładu który mi tłumaczyliscie

Gray: To będzie wyglądało jak ... wiatrak z trzema ... skrzydłami (? − co ma wiatrak?)

floridaa: no tak ale np. π<arg(z³)<3π/2.... rozpisuje to na π−2kπ/3<argz<3π/2 − 2kπ/3 , może tak być ?

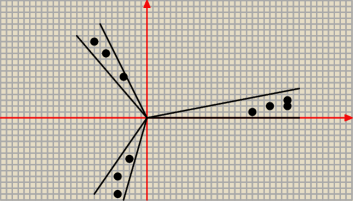
Gray: Twoje to te obszary z kropkami.

floridaa: a jakie k podstawiasz ?

Gray: Nie może, nie podzieliłaś wszystkiego przez 3.

floridaa: dobra już wiem ... dzięki wielkie ... gapa ze mnie niesamowita jak bd miała problem jeszcze z jakimś przykładem to sie odezwe tu mam nadzieje że pomożecie bo jutro kolokwium i musze to ogarnąć ...

floridaa: o a jeszcze taki przykład {z∊C: Im(z³)> Re (z³)} jak takie coś rozpisać

Gray: z=|z|(cosα+isinα) ⇒z³=|z|³(cos3α+isin3α) Im(z³)>Re(z³) ⇔ sin3α>cos3α rozwiąż tę nierówność, otrzymasz α należące do pewnych przedziałów. Wybierz te, które leżą w okresie, tj w [0,2π). I narysuj jak w poprzednik zadaniu (bo α=argz).

floridaa: obliczyć (cos π/3− i sin π/3) ⁷ ?

Gray: Możesz Dlaczego mnie pytasz?

floridaa: no wiem że moge ale nie potrafie xD hah już tydzień siedze nad tym wszystkim i dlatego pisze tu na forum bo nigdzie nie moge znaleźć jakiejkolwiek pomocy ..

Gray: ... = (cos (−π/3) + i sin (−π/3))⁷ = wzór de Moivre'a = (cos (−7π/3) + i sin( −7π/3)) = = (cos (7π/3) − i sin(7π/3)) = cos( π/3) − isin( π/3) = ...

floridaa: jeszcze wróciłabym do tej nierówności bo z nią nie mogę sobie poradzić

Gray: sinx>cosx ⇔ x∊(π/4 + 2kπ, 5π/4 +2kπ) Zatem sin3α>cos3α ⇔ 3α∊(π/4 + 2kπ, 5π/4 +2kπ) ⇔ α∊(π/12 + 2kπ/3; 5π/12 +2kπ/3), k=0,1,2

floridaa: dziękuje Ci bardzo, a skąd wzięła sie zależność że jesli sinx>cosx⇔ x∊(π/4+2kπ, 5π/4+2kπ) ?

Gray: Narysuj te dwie funkcje w jednym układzie współrzędnych i zobacz kiedy sin jest nad cos.

floridaa: dziękuje Ci bardzo za wszystkie odpowiedzi i za cierpliwość

Gray: Proszę

floridaa: jesteś moim mistrzem

Gray: Bądź więc moją Małgorzatą