funkcje Dusia: naszkicuj wykres funkcji która spełnia nastepujące trzy warunki: *ma dokładnie 2 miejsca zerowe x=−1 i x=5 *wartości dodatnie przyjmuje dla argumentów większych od −1 i jednocześnie mniejszych od 5 *wartości ujemne przyjmuje dla argumentów mniejszych od −1 oraz dla argumentów większych od 5

ula: słuchaj to jest zwykla parabola, ramiona do dołu

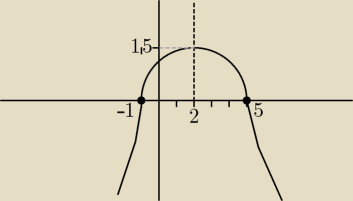
Godzio: trzeba wyznaczyć wierzchołek: wiemy że ma 2 Mz czyli piszemy postać kanoniczną y=−a(x+1)(x−5) wymnażamy (a jest ujemne) y=−a(x²−5x+x−5) y=−ax²+4ax−5a a=−a b=4a c=−5a Δ=16a²−20a²=−4a²

	−4a+4a2
x1=
	−2a

2a=−4a+4a² 6a=4a² 6=4a a=1,5 obliczamy współrzędne wierzchołka:

	−4a
xw=		=2
	−2a

	−Δ		4a2		9
yw=		=		=		=1,5
	−4a		−4a		−6

Mam nadzieję że jest to poprawnie rozwiązane

Godzio:

	9
na koncu
	6

Godzio:

	−Δ		4a2		9
yw=		=		=		=1,5
	4a		4a		6

Miś: Wcale nie musi to być parabola To może być f(x) = (x + 1)(x − 5) * g(x) gdzie g(x) > 0 dla każdego x np: f(x) = (x + 1)(x − 5) * (x + 2)² f(x) = (x + 1)(x − 5) * (sin(x) +1,5)