Geometria analityczna Analiza: Punkty A(5, 1) oraz B(1, 5) są symetryczne względem prostej k. Prosta k ma równanie: Prawidłowa odpowiedź: x − y = 0 Co to za czary? Jak? Na podstawie? Mógłby mi ktoś wytłumaczyć jak do tego dojść? Tak samo z zadaniem: Odległość punktu A(a, −3) od prostej y = x jest równa √2. Wskaż zdanie prawdziwe: (Odnosi się do ilości liczb a spełniających warunki zadania) Poprawna odpowiedź: Istnieją dwie liczby a₁ i a₂, spełniające warunki zadania, które są rozwiązaniami równania a²+6a+5=0

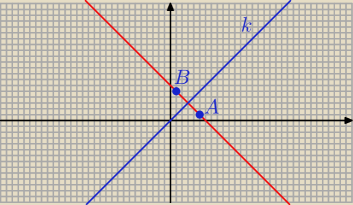
Janek191: A = ( 5; 1) B = ( 1; 5) Wyznaczamy prostą AB

	y2 − y1		5 − 1
a =		=		= − 1
	x2 − x1		1 − 5

y − y₁ = a*( x − x₁) y − 1 = − 1*( x − 5) y − 1 = − x + 5 y = − x + 6 ========== S − środek odcinka AB S = (3; 3) k − symetralna odcinka AB czyli jest do niego prostopadła i przechodzi przez jego środek: y = x + b 3 = 3 + b b = 0 więc y = x Odp. x − y = 0 =======

Janek191: z.2 y = x x − y + 0 = 0 A = ( a ; − 3) d = √2 Korzystamy z wzoru na odległość punktu od prostej :

	I A xo + B y0 + C I
d =		P = ( x0; y0}
	√A2 + B2

Po podstawieniu danych otrzymamy

	I 1*a + (−1)*(−3) + 0 I
		= √2
	√ 12 + (−1)2

I a + 3 I
	= √2 / *√2
√2

I a + 3 I = 2 a = − 5 lub a = − 1 −−−−−−−−−−−− spr. a² + 6 a + 5 = 0 ( a + 5)*( a + 1) = 0 a₁ = − 5 oraz a₂ = − 1 =========================

Analiza: Okej, dzięki, zajarzyłem. Problem w tym, że nie wiedziałem o istnieniu tego wzoru na odległość punktu od prostej, a na tej stronie widnieje on w materiale dla rozszerzenia, natomiast znalazłem go w moim podręczniku dla podstawy.

Analiza: A nie, jednak dalej nie wiem, bo na podstawie nie ma wartości bezwzględnej i nie wiem jak obliczyć | a + 3 | = 2 No geniusz współczesnej edukacji, dać wzór, gdzie jest element, którego nie ma na podstawie.

Janek191: Wartość bezwzględna była w VI klasie szkoły podstawowej w latach osiemdziesiątych

Janek191: I a + 3 I = 2 a można odgadnąć I − 1 + 3 I = I 2 I = 2 I − 5 + 3 I = I − 2 I = 2