Rozwiąż nierowność. Wartość bezwzględna. Zeco:

	|2x−2|
Rozwiąż nierowność		>4
	|x−4|

Rozpatruje ją w 3 przypadkach gdy: 1) x nalezy do przedzialu (−nieskonczonosc,1), tu wychodzi mi zbior pusty 2) <1,4) tu <1,4) 3) <4, nieskonczonosć) i tu pusty. Gdzieś robie bład ale nie potrafie go zlokalizowac, ponieważ moj wynik nie jest zgodny z odpowiedzią autora. Chyba ze autor sie myli W koncu tez człowiek Prosze was o pomoc i rozpisanie tego w sposob dosyc prosty.

ICSP: D : x ≠ 4

|x − 1|
	> 2
|x−4|

(x−1 − 2x + 8)(x − 1 + 2x − 8) > 0 (−x + 7)(3x − 9) > 0 (x−7)(x−3) < 0 x ∊ (3 ; 7) \ {4}

Zeco: Możesz mi to tak rozpsiac jeszcze troszke prosciej po kolei w danym przedziale bo ww zapis ciezko mi ogarnac

PW: |2x−2| = 2|x−1|, a więc nierówność ma równoważną postać

	|x−1|
		> 2,
	|x−4|

a ponieważ

	|a|		a
		= |		|, b≠0,
	|b|		b

mamy

	x−1
|		| > 2, x≠4
	x−4

	x−4+3
|		| > 2
	x−4

	3
|1+		| > 2
	x−4

	3		3
− 2 < 1+		∨ 1+		> 2
	x−4		x−4

	3x − 9		−(x−7)
0 <		∨		> 0
	x−4		x−4

3(x−3)(x−4) > 0 ∨ (x−7)(x−4} < 0

Zeco: Nie wiem, dalej tego nie kumam

pigor: ..., to może jeszcze np. tak: :

|2x−2|
	>4 /*|x−4| i x−4≠0 ⇔ 2|x−1| >4|x−4| /:2 i (*)x≠4 ⇒
|x−4|

⇒ |2x−8|<|x−1| ⇔ 2x−8<x−1 i 2x−8>1−x ⇔ x<7 i x>3 ⇔ 3< x< 7, a stąd i z (*) ⇔ x∊(3;4) U (4;7) . ...

pigor: ..., a co do sposobu ICSP z godz 15:13 to

|2x−2|		|2(x−1)|
	>4 i x−4≠0 ⇔		>4 /*|x−4| i (*) x−4 ⇒
|x−4|		|x−4|

⇒ 2|x−1| >4|x−4| /:2 ⇔ |x−1| >2|x−4| /² obustronnie ⇔ |x−1|² >|2x−8|² ⇔ ⇔ (x−1)²−(2x−8)² >0 ⇔ (x−1−2x+8)(x−1+2x−8) >0 ⇔ (−x+7)(3x−9) >0 ⇔ ⇔ −3(x−7)(x−3) >0 /:(−3) ⇔ (x−7(x−3) <0 ⇔ 3<x<7 , stąd i z (*) ⇔ ⇔ x∊(3;7)\{4} ⇔ x∊(3;4) U (4;7) . ...

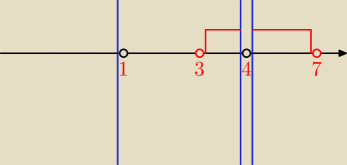
Bogdan: Proponuję taki zapis:

|2x − 2|
	> 4 /*|x − 4| ⇒ 2|x − 1| > 4|x − 4| ⇒ |x − 1| > 2|x − 4| i x≠4
|x − 4|

dla x∊(=∞, 1): −x + 1 > −2x + 8 ⇒ x > 7 sprzeczność bo x < 1 dla x∊<1, 4): x − 1 > −2x + 8 ⇒ 3x > 9 ⇒ x > 3, x∊<(3, 4) dla x∊(4, +∞): x − 1 > 2x − 8 ⇒ x < 7, x∊(4, 7) Odp.: x∊(3, 4)∪(4. 7)

Zeco: Dzieki wielkie, teraz po spokojnym przeanalizowaniu wszystkich waszych sposobów juz rozumiem. Naprawde bardzo wam dziekuje

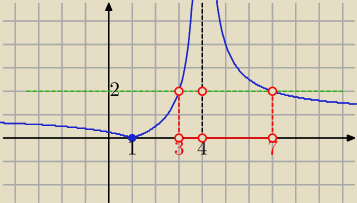
Eta: x≠ 4

	2(x−1)		x−1
|		|>4 ⇒|		|>2
	x−4		x−4

	x−1		3
1/ rysujemy wykres f(x)=|		| = |1+		|
	x−4		x−4

2/ y=2 f(3)=2 i f(7)=2 i x≠4 f(x) >2 ⇒x∊(3,4) U (4,7)