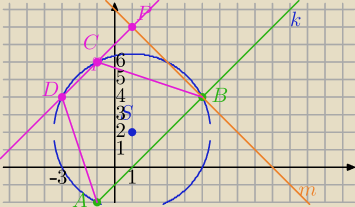
Ostatnia szansa Code::Blak: W okręgu o równaniu (x−1)² + (y−2)² = 20 wpisano trapez równoramienny. Dłuższa podstawa trapezu jest zawarta w prostej x− y = 1 Wyznacz współrzędne wierzchołków trapezu, jeśli jego wysokość jest równa 4√2 Obliczyłem że podstawa ma A(−1,−2) i B (5,4)

Mila: (x−1)² + (y−2)² = 20 S=(1,2), r=2√5 Punkty przecięcia okręgu i prostej: (x−1)²+(x−3)²=20 x−y=1⇔k: y=x−1 x=−1 lub x=5 y=−2 lub y=4 A(−1,−2),B=(5,4) C jest odległy od prostej k o 4√2. m⊥k i B∊m y=−x+b, 4=−5+b, b=9 m: y=−x+9 Szukamy na prostej m punktu P odległego od k o 4√2 P(x,−x+9) ∊m k: x−y−1=0

|x−(−x+9)−1|
	=4√2 /*√2⇔
√12+12

|2x−10|=8 2x−10=8 lub 2x−10=−8 2x=18 2x=2 x=9 lub x=1 y=0 P=(9,0) nie odpowiada war. zadania ( napisz dlaczego) lub y=−1+9=8 P=(1,8) Piszemy równanie prostej n równoległej do k i P∊n, k: y=x−1 y=x+b. 8=1+b, b=7 n: y=x+7odstawiamy do równania okręgu: (x−1)² + (x+7−2)² = 20 stą d x=−1 lub x=−3 y=6 lub y=4 C=(−1,6) D=(−3,4)