:D Force: Witam proszę o wyjaśnienie tego zadania: Dana jest parabola o równaniu y=x²+1 i leżacy na niej punkt A o współrzędnej x=3. Wyznacz równanie stycznej do tej paraboli w punkcie A

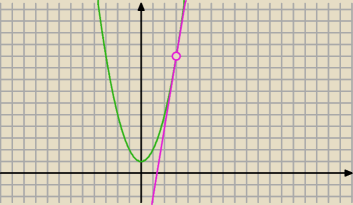
Tadeusz: y_A=10 A=(3,10) y'=2x y'(3)=6 l: y−10=6(x−3) ⇒ l: y=6x−8

Arkusz: A (3;10) y = ax + b 10 = 3a + b b = 10 − 3a zatem y = ax + 10 − 3a przyrównujemy parabole i prostą x² + 1 = ax + 10 − 3a x² − ax − 9 + 3a = 0 Chcemy by przecieły sie w jednym punkcie zatem Δ = 0 Δ = a² + 4(9 − 3a) Δ = 0 a² − 12a + 36 = 0 (a − 6)² = 0 a = 6 ⇒ b = −8 y = 6x − 8