parabola okrąg
Karolina: mamy okrąg x
2+(y−3)
2=5. znaleźć równanie paraboli postaci y=ax
2 stycznej
do tego okręgu.
zrobiłam to tak:
x
2+(y−3)
2=5
y=ax
2
x
2+(ax
2−3)
2=5
a
2x
4+(1−6a)x
2+4=0
x
2=t
a
2t
2+(1−6a)t+4=0
Δ=0
20a
2−12a+1=0
Δ=64
√Δ=8
i co dalej? proszę o wskazówki/podpowiedź
11 lis 17:52
Karolina: a to co ja robiłam to jest źle?
przepraszam, ale niestety nic nie zrozumiem z Twojego zapisu
| | 1 | |
a wiem, ze odp ma byc y= |
| x2 |
| | 2 | |
11 lis 18:09
Eta:
Sorry,źle przeczytałam treść zadania
11 lis 18:16
Tadeusz:
...Ty tylko zabłądziłaś na ścieżce ... całkiem dobrze szłaś ....tylko nie wiesz gdzie
doszłaś−

(pominęłaś założenie dla t)
A nasz miła
Eta ... przekombinowała −

11 lis 18:16
Eta:

11 lis 18:16
Karolina: dobra juz wiem co robiłam, mam to założenie dla t
moze glupie pytanie, ale jak mam je teraz wprowadzic w moje rozwiazanie?
11 lis 18:18
Tadeusz:
−

hej
Lwico−Alfa
11 lis 18:19
Karolina: pomoż, prosze
11 lis 18:20
Eta:
Hej "Bizon"

Aaaaaaa to Ty "żenicho"

a tak długo myślałam ?
11 lis 18:22
Karolina: pomoże mi ktoś co dalej z tym moim rozwiazaniem?
11 lis 18:24
Tadeusz:
... ha...ha...ha ...
...
===
11 lis 18:25
Karolina: pomoże ktos?
11 lis 18:30
Karolina: chociaż dlaczego w rozwiązaniu jest odrzucone to pierwsze rozwiązanie, czyli a1?
11 lis 18:31
Tadeusz:
... zapomniałaś względem jakiego argumentu liczysz równanie −

11 lis 18:36
Karolina: chyba naprawdę się pogubiłam.
możesz powiedzieć mi co dalej powinnam zrobić w tym zadaniu?
11 lis 18:43
Karolina: bardzo proszę, bo już nie mam siły do tego typy zadań
11 lis 18:52
Karolina: proszę proszę proszę x100000000000000000
11 lis 19:01
Tadeusz:
jesteś tu:
x2=t gdzie t>0
11 lis 19:05
Tadeusz:
a
2t
2+(1−6a)t+4=0
miałaś wybór ...ale zdecydowałaś, że rozwiązujesz względem t
Wyliczyłaś, że Δ=0 dla a
1=1/10 a
2=1/2
Wracasz do równania wyjściowego i dla a
1 otrzymujesz
t
2/100+4t/10+4=0
(t/10+2)
2=0 ⇒ t=

? sprzeczne z założeniem t>0
11 lis 19:12
Tadeusz:
dla a2 otrzymujesz:
t2/4−2t+4=0
(t/2−2)2=0 t/2=2 t=4
zauważ, że x1=−2 x2=2 są współrzędnymi punktów styczności
11 lis 19:16
Tadeusz:
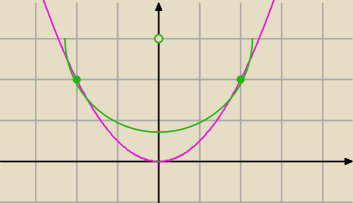
11 lis 19:19
Karolina: bardzo Ci dziękuję
naprawdę mi pomogłeś, jeszcze raz bardzo dziękuję

11 lis 19:24
Karolina: jestem bardzo wdzięczna za pomoc
dziękuję

!

11 lis 19:24
Tadeusz:
−

11 lis 19:28
 (pominęłaś założenie dla t)
A nasz miła Eta ... przekombinowała −
(pominęłaś założenie dla t)
A nasz miła Eta ... przekombinowała −

 hej Lwico−Alfa
hej Lwico−Alfa
 Aaaaaaa to Ty "żenicho"
Aaaaaaa to Ty "żenicho"  a tak długo myślałam ?
a tak długo myślałam ?

 ? sprzeczne z założeniem t>0
? sprzeczne z założeniem t>0


 !
! 
