Pomoc w dokończeniu zadania z wielomianem świeżak: Dany jest wielomian W(x)=x⁴−mx³+nx²−8 . Wartość tego wielomianu dla x=2 jest taka sama jak dla x=−2. Natomiast W(3)=82. Wyznacz wartości liczb m i n oraz rozwiąż nierówność W(x)>x⁴+2. Po obliczeniach wychodzi x²−8>2 i ja zrobiłbym to tak: x²>10 x>√10 x∊(√10,+∞) ale podobno trzeba to zrobić w ten sposób: x²−8−2>0 x²−10>0 a więc ze wzoru skróconego mnożenia (x−√10)(x+√10)>0 Pytanie może śmieszne, ale jak to zinterpretować? x∊? Jeśli ktoś odpowie to byłbym wdzięczny za objaśnienie dlaczego właśnie tak jest, czyli dlaczego taka interpretacja i dlaczego ja robiłem to źle

eba: Widzisz, intuicyjnie założyłeś, że jak spierwiastkujesz 10, to dostaniesz √10. Ale możesz dostać też −√10. Więc lepiej pisz wersję poprawną th x²−10>0 = (x−√10)(x+√10)>0

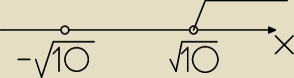
świeżak: faktycznie pominąłem −√10 przy pierwszym sposobie, ale co z interpretacją (x−√10)(x+√10)>0 ? z odpowiedzi wynika, że rozwiązaniem jest x∊(−∞;−√10)∪(√10;+∞) ale dlaczego? skoro nierówność musi być większa od 0 do żaden z nawiasów nie może równać się 0 a więc x−√10≠0 oraz x+√10≠0 więc x≠√10 i podobnie z drugim nawiasem x≠−√10, no ale dlaczego x∊(−∞;−√10)∪(√10;+∞)? może ktoś podpowie (√10;+∞) może wynikać z tego że nierówność jest większa od 0 czyli x>√10 więc zbiór rozwiązań na osi leci w prawo (jak na rysunku), ale skąd wziął się (−∞;−√10)? wydaje mi się, że skoro nierówność jest większa od 0 to też powinien lecieć w prawo ale wtedy wychodziło by, że x∊(−√10;√10)∪(√10;+∞) niestety inaczej niż powinno

PW: Narysuj parabolę, to się wyjaśni (usiłujesz rozwiązać nierówność kwadratową w oderwaniu od tej funkcji kwadratowej, medytując nad argumentami na osi OX, czyli mówiąc nie na temat).

świeżak: no i się wyjaśniło, dzięki wielkie −> −>