Ciągi Blue: Byłabym Wam bardzo wdzięczna, gdybyście mi sprawdzili, czy dobrze to obliczyłam

	5−n
zad.1 Udowodnij, że ciąg określony wzorem an =		jest ciągiem malejącym.
	2n+3

http://pl.tinypic.com/view.php?pic=bhheg7&s=8#.VGHzCJrxIiQ zad.2 Niech f(x) = 1+x+x²+x³+... będzie sumą szeregu geometrycznego zbieżnego. Udowodnij, że

	1
zbiorem wartości funkcji f jest przedział (		, ∞).
	2

http://i60.tinypic.com/hx6i46.jpg zad.3 Ciąg (a_n) określony jest wzorem a_n = 3²ⁿ⁺¹−9ⁿ⁻¹. Udowodnij, że ten ciąg jest geometryczny. http://i58.tinypic.com/nfqi6v.jpg zad.4 Udowodnij, że jeśli liczby a i b spełniają warunek |a|≠|b|, to liczby (a+b)², a²−b², (a−b)² w podanej kolejności tworzą ciąg geometryczny. http://pl.tinypic.com/view.php?pic=97lnys&s=8#.VGHymprxIiQ zad.5 Udowodnij, że jeśli liczby a,b,c tworzą ciąg arytmetyczny, to także liczby : a²+ab+b², a²+ac+c², b²+bc+c² w podanej kolejności tworzą ciąg arytmetyczny. http://pl.tinypic.com/view.php?pic=rbjxat&s=8#.VGHyYprxIiQ Mam jeszcze problem z tym zadaniem : zad.10 Wyznacz wszytkie wartości parametru m dla których cztery różne pierwiastki równania x⁴−10x²+m=0 tworzą ciąg arytmetyczny

Kacper: W 1 nie podoba mi się uzasadnienie, że 4n²+16n+15>0 Ty to zakładasz z góry? Tak nie można. W ogóle zbędne to liczenie delty, bo dla n∊N₊ każdy składnik jest dodatni, czyli suma jest dodatnia.

Kacper: W drugim co znaczy Q (a) Poza tym myślę, że może być (Ja znowu wolałbym dowód algebraiczny, ale przymknę oko )

Kacper: Zadanie 3 Najpierw dowodzisz, że ciąg jest geometryczny, a na końcu piszesz coś przeciwnego Poza tym ogólnie przyjęło się, że iloraz nie (iloczyn) ciągu geometrycznego oznaczamy małą literą alfabetu q

Kacper: Zadanie 4 gdzieś obcięte, ale ogólnie ok. Zastanawiałaś się po co to założenie było?

Kacper: Zadania 5 nie chce mi się czytać, ale idea dobra

Blue: zad.1 no ale przecież wyliczyłam pierwiastki i gołym okiem widać, że dla liczb naturalnych jest wartość dodatnia zad.2 jakie Q(a) − ja tam nic takiego nie widzę zad.3 Sorry iloraz, pomyliłam Ale jak to piszę coś przeciwnego Co ja przeciwnego napisałam zad.4 Szczerze, nie zastanawiałam się zad.5 Czyli uznam, że jest dobrze

Blue: Kacper co do tego q , to ja tak piszę małe q xD Jakoś nigdy nie umiałam tego pisać

Kacper: W zadaniu czwartym m=9?

Kacper: W drugim tam chyba jest q∊(−1,1)

Blue: Chodzi Ci o zadanie 10? tak, wyjdzie m= 9 i m=0 − ale nie wiem, jak to liczyć.... Powiedz mi jeszcze co jest źle w tym 3 zadaniu

Blue: tak ^^

Kacper: No wszystko dobrze ogólnie, tylko zdanie ostatnie to totalna bzdura

Blue: Jak mogłeś pomylić zapis q∊(−1,1) z Q (a) ?

Blue: Ale jak to? Jakbym napisała iloraz, zamiast iloczyn, to przecież wszystko byłoby dobrze, prawda?

Kacper: W zadaniu 10 nie może być m=0, bo wtedy równanie nie ma 4 różnych pierwiastków

Kacper: Tak, jak zamienisz te słowa, to będzie ok

Blue: To czyli git A wytłumaczysz mi to zad.10, bo ja mam m=0 w odpowiedziach, ale jak już dobrze wiemy w tej książce zdarzają się błędy

Kacper: Przykładowe rozwiązanie: Skoro równanie ma 4 różne pierwiastki, to x⁴−10x²+m=(x−x₁)(x−x₂)(x−x₃)(x−x₄) Dodatkowo mają one tworzyć ciąg arytmetyczny, czyli x₁=a x₂=a+r x₃=a+2r x₄=a+3r (oczywiście r≠0, bo pierwiastki różne) Porównujemy x⁴−10x²+m=(x−a)(x−(a+r))(x−(a+2r))(x−(a+3r)) Wymnażamy i rozwiązujemy układ równań. Dostaniemy a=−3, r=2 lub a=3,r=−2 I jak policzymy, to m=9 Sporo rachunków. Zapewne zastosowanie wzorów Viete'a mogłoby uprościć sprawę, tylko że ich w programie nie ma

Blue: Cooo? Przecież wzory Vietea są w programie

Blue: Ale Kacper powiedz mi, gdzie Ty tutaj masz ten układ?

Kacper: Dla równań 4 stopnia nie jak wymnożysz tego potworka z prawej, czyli (x−a)(x−(a+r))(x−(a+2r))(x−(a+3r)) to dostaniesz dwa wielomiany. Jak wiadomo współczynniki przy tych samych potęgach muszą być równe, stąd układ równań

Asay: Wzory Viete'a 4 stopnia. To jest to !

Blue: A no tak, dziękuję Kacper

Blue: Kacper, na pewno nie ma prostszego sposobu, mylę się przy tych obliczeniach...

Mila: O które zadanko chodzi? Tyle komentarzy, to nie chcę szukać.

Blue: Mila, o zadanie 10

Blue: to ostatnie

Kacper: Będę miał chwilę czasu to pomyślę

Blue: Będę wdzięczna

Mila: Po kolacji wezmę się za 10 zadanie. R−ka wyszła Ci znośnie, jeśli będziesz dalej tak solidnie pracować,( może dam wskazówki, co zmienic w stylu pracy), to będzie w maju powyżej 75.

Blue: Mila o takim wyniku to nawet mi się nie śni, ale rady chętnie poczytam

Kacper: Mila witam O ile nie dadzą czegoś "nowego"

Martiminiano: Też chętnie owe rady przeczytam.

Mila: 1) Wyznacz wszystkie wartości parametru m dla których cztery różne pierwiastki równania (*) x⁴−10x²+m=0 tworzą ciąg arytmetyczny. x²=t t²−10t+m=0 Δ=100−4m>0⇔m<25 t₁+t₂>0 i t₁*t₂>0 [ otrzymamy 4 różne pierwiastki równania (*)] (**) t₁+t₂=10>0 i t₁*t²=m ⇔m>0⇔ m∊(0,25)

	10−2√25−m		10+2√25−m
t1=		lub t2=
	2		2

t₁=5−√25−m lub t₂= 5+√25−m t₁<t₂ Otrzymamy 4 różne rozwiązania : √t₁,−√t₁,√t₂, −√t₂ Zauważ, że √t₁,−√t₁ to liczby symetryczne względem OY √t₂, −√t₂ tak samo Ustawiamy je na osi liczbowej: −√t₂,−√t₁,√t₁, √t₂ Z założenia mają tworzyć ciąg arytmetyczny:

	−√t2+√t1		√t2−√t1
⇔,−√t1=		i √t1=		⇔
	2		2

−3√t₁=−√t₂ i 3√t₁=√t₂⇔ √t₂=3√t₁ ⇔t₂=9t₁ podstawiamy do (**) t₁+t₂=10 t₁+9t₁=10 t₁=1 podstawiamy do t₁*t₂=m t₁*9t₁=m 1*9*1=m m=9 Sprawdzenie zostawiam Tobie.

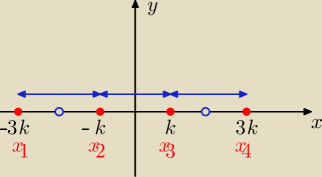
Eta: x⁴−10x²+m=0 dla m=0 x⁴−10x²=0 ⇒ x²(x²−10)=0 ma trzy różne pierwiastki( nie spełnia treści zad.) równanie x⁴+bx²+c=0 ma cztery różne pierwiastki, to są one położone na osi OX symetrycznie względem OY i dodatkowo mają tworzyć ciąg arytmetyczny zatem odległość między nimi jest taka sama wprowadzam oznaczenia x₁= −3k , x₂= −k, x₃= k, x₄=3k z postaci iloczynowej (x+3k)(x+k)(x−k)(x−3k)=0 ⇒ (x²−k²)(x²−9k²)=0 ⇒ x⁴−10k²+9k⁴=0 i x⁴−10x²+m=0 zatem: −10k²= −10 i 9k⁴=m k²=1 to k⁴=1 ⇒ m=9

Kacper: No i już mogę mój czas przeznaczyć dla moich "dzieci" Eta dla ciebie też

Eta:

Eta: Kacper a co robi "żona" ? że Ty zajmujesz się "dziećmi"

Eta: Poprawiam chochlika: ........ ⇒ x⁴−10k²x²+9k⁴=0

Blue: Omg, Mila , jesteś geniuszem ^^ Dzięki wielkie

Blue: Eta, Tobie też dziękuję

Blue: Mila, a co z tymi radami?

Mila: Będą , w trakcie problemów. Pracuj spokojnie.

Blue: ok