Wyznacz zbiór A∩B A∪B A\B, gdzie
ignorantia: Czy ktoś mógłby mi pokazać, co zrobić z tymi x
4 i x
5
A={x∊ℛ,
√x+4>3} B={x∊ℛ,
x4x≤8
A={x∊ℛ,
x52x>0} B={x∊ℛ, |x−1|≤5}
11 lis 12:00
J :
| | x4 | |
rozwiązać nierówność: |
| ≤ 8 ... podobnie x5 ... |
| | x | |
11 lis 12:07
ignorantia: Problem polega na tym, że nie wiem jak ją rozwiązać.
11 lis 12:09
J :
założenie: x ≠ 0 ...x3 ≤ 8 ⇔ x ≤ 2.... i x ≠ 0 ...
11 lis 12:12
ignorantia:
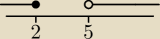
Czyli w pierwszym przypadku będzie to wyglądało tak?
A=
√x+4>3/
2
x+4>9
x>5
A=(5,+
∞)
B=
x4x≤8
x
3=2
3
x=3
B=(−
∞,2>
A∩B (−
∞,+
∞)
A∪B ∅
A\B <2,5)
11 lis 12:33
J :
liczba x = 0 ..nie należy do zbioru B..
11 lis 12:37
ignorantia: Czyli ma być
B= (−∞,0> <0,2>
A∩B (−∞,0> <0,+∞)
A\B <5,+∞)
11 lis 12:46
J :
B = (−∞,0) u (0,2> ...
11 lis 12:47
ignorantia: Ok, dzięki. A co z x52x>0?
doszedłem tylko do tego, że x≠0 i x5+1>2x
11 lis 12:52
J :
| | x4 | |
x ≠ 0 ... |
| > 0 ⇔ x4 > 0 ⇔ x ≠ 0 ....B = R/{0} |
| | 2 | |
11 lis 12:55
ignorantia: Przepraszam. Wkradł się błąd.
Porprawnie jest x5+12x>0
11 lis 12:58
 A={x∊ℛ, √x+4>3} B={x∊ℛ, x4x≤8
A={x∊ℛ, x52x>0} B={x∊ℛ, |x−1|≤5}
A={x∊ℛ, √x+4>3} B={x∊ℛ, x4x≤8
A={x∊ℛ, x52x>0} B={x∊ℛ, |x−1|≤5}
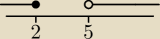 Czyli w pierwszym przypadku będzie to wyglądało tak?
A= √x+4>3/2
x+4>9
x>5
A=(5,+∞)
B= x4x≤8
x3=23
x=3
B=(−∞,2>
A∩B (−∞,+∞)
A∪B ∅
A\B <2,5)
Czyli w pierwszym przypadku będzie to wyglądało tak?
A= √x+4>3/2
x+4>9
x>5
A=(5,+∞)
B= x4x≤8
x3=23
x=3
B=(−∞,2>
A∩B (−∞,+∞)
A∪B ∅
A\B <2,5)