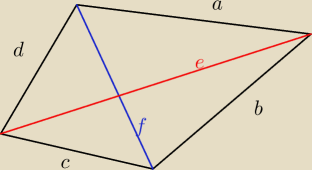
nierówności trójkąta Michał: uzasadnij, że suma długości przekątnych dowolnego czworokąta wypukłego jest większa od połowy obwodu Wydaje mi się że wynika to z nierownosci w trojkacie : długosz najdluzszego boku < suma dlugosci krotszych bokow, czyli : e < a+d i e < b +c f < a+b i f <c+d

⎧	2e < a +b+c+d
⎩	2f < a+b+c+d

2(e+f) < 2(a+b+c+d) Nie wiem co dalejj zrobić ...

Michał: ...?

pigor: .., twoje nierówności w porządku i wykazałeś, że e+f< a+b+c+d czyli suma przekątnych czworokąta jest jest mniejsza od jego obwodu, a my mamy wykazać, że ta suma jest większa od jego obwodu, no to aby wykorzystać twój rysunek niech punkt przecięcia przekątnych e i f dzieli je tak: e na części x i e−x, zaś f na y i f−y, więc z nierówności trójkąta na tym rysunku masz układ 4−ech nierówności np. taki : −−−−−−−−−−−−−−−−−−−−−− x+y >c i y+e−x >b i e−x+f−y >a i f−y+x >d /+ stronami ⇒ x+y+y+e−x+e−x+t−y+f−y+x > c+b+a+d ⇔ 2(e+f) > a+b+c+d ⇔ ⇔ e+f > ¹₂(a+b+c+d) ..., c.n.w.

Michał: dzięki

pigor: .... tam w moim komentarzu do rozwiązania powinno być nie ...." większa od jego obwodu ", tylko "większa od połowy jego obwodu"

Eta: dla π...

pigor: ..., miło i słodko, dzięki η