Rozwiązywanie trójkątów met. trygonometryczną Damian: W czwartek mam poprawę pracy klasowej z trygonometrii. Dostałem masę zadań, a przy niektórych z nerwów wypadają mi już włosy . Będę ogromnie wdzięczny za pokazanie jak rozwiązać poniższe zadania. Jeśli komuś się uda, to zdobędzie moje szczere uznanie, bo szukałem po całym internecie i nic nie znalazłem (natknąłem się tylko na różne wzory, które jednak na nic się zdały). Jest to teoretycznie poziom podstawowy przygotowujący do nowej matury. 1. Wyznacz długości boków trójkąta prostokątnego ABC, (kąt C jest prosty) mając dane: a = 2 − √2 b = 2√3 − √6 Powinno wyjść: c = 4 − 2√2 2. W trójkącie równoramiennym dane są: długość podstawy 10 cm i kąt przy podstawie równy 30°. Oblicz długość promienia koła wpisanego w trójkąt i promienia koła opisanego na tym trójkącie. Prawidłowa odp.:

	10√3
R =		cm
	3

r = 5 (2 − √3) cm 3. Pole trójkąta równoramiennego wynosi 16 cm². Oblicz miarę kąta między ramionami tego trójkąta, jeżeli jego ramię ma długość 8 cm. Odp.: 30° lub 150°

Damian: Jak coś wiem, że w zadaniu pierwszym wystarczy użyć tw. Pitagorasa, ale wychodzą mi takie pierwiastki, które ani trochę nie są zbliżone do odpowiedzi.

Eta: No to jak tak dalej pójdzie , to będziesz "łysym 20−latkiem" 1/ tw. Pitagorasa c²=a²+b² b= 2√3=√6= 2√3−√3*√2= √3(2−√2 c²= (2−√2)²+3*(2−√2)²= 4*(2−√2)² c= 2*|2−√2|= 4−2√2

Mila: c²=a²+b² c²=(2−√2)²+(2√3−√6)² c²=2²−2*2√2+(√2)²+(2√3)²−2*2√3*√6+√6² c²=4−4√2+2+4*3−4√18+6 c²=24−4√2−4*√9*2 c²=24−4√2−4*3√2 c²=24−16√2 c²=4*(6−4√2)=4*(2−√2)² c=√4*√(2−√2)²=2*(2−√2) c=4−2√2 ==========

Eta:

Eta: 3/ P=16

	1
i P=		*8*8*sinα = 32sinα , α∊(0o,180o)
	2

	1
to: 32sinα= 16 ⇒sinα=		⇒ α=30o lub α= 180o−30o= 150o
	2

Eta: I co? żyjesz? Pewnie wszystkie włosy zgubił i się załamał biedaczek

Damian: Wybaczcie, że tak długo, ale wciągnąłem się w wir nauki . Jak się człowiek uczy cały dzień, to te godziny lecą jak oszalałe. Nie pomyślałbym, że to takie proste . Aż mi wstyd, ale na szczęście matura czeka mnie dopiero w przyszłym roku szkolnym (w 4. klasie technikum) . Może w międzyczasie odnajdę gdzieś swój potencjał matematyczny, którego na razie próżno u mnie szukać Jak sam rozwiązywałem 1., to zatrzymałem się na 24 − 16√2 (tak jak rozwiązała Mila) i nie wiedziałem co dalej . Za nic bym nie pomyślał, że to można tak rozłożyć, żeby wyszedł skrócony wzór mnożenia. W 3. zupełnie zapomniałem o wzorze na pole z użyciem kąta. Pewnie nawet jakbym sobie

	1
przypomniał, to i tak nie wiedziałbym co dalej, bo w książce mam, że P =		* ab * sinα,
	2

gdzie a jest podstawą trójkąta, a b ramieniem. A ty pomnożyłaś ramiona i tyle . Zostało jeszcze 2 zadanie. Nie wiem jak ten promień koła wyliczyć. Niby w internecie znalazłem wzory, ale jak je zastosowałem, to wyszły mi jakieś dziwne liczby.

	2P
r =
	a+ b + c

	abc
P =
	4R

To są znalezione wzory na promień koła wpisanego w trójkąt równoramienny.

Damian: Koło wpisane w trójkąt równoramienny a − podstawa c − ramię h − wysokość a = 10 Kąt przy podstawie = 30^o

	√3
tg30o =
	3

√3		h
	=
3		5

3h = 5√3

	5√3
h =
	3

	√3
cos30o =
	2

√3		5
	=
2		c

c√3 = 10 / :√3

	10		10√3
c =		=
	√3		3

To już dawno wypisałem w zeszycie. Podstawa jest, ramiona są, podstawowe kąty też. Instynkt mi mówi, że to prostsze niż myślę, ale rozum nie daje wskazówek . Tylko te nieszczęsne koło jest puste. Próbowałem wpisać w ten trójkąt mniejsze trójkąty prostokątne, żeby dojść do promienia koła, ale nic mi to nie dało. Pamiętam, że w gimnazjum takie zadania rozwiązywałem. Aż nie mogę uwierzyć, że teraz się z tym męczę . PS.: Z tymi włosami żartowałem, nie wypadają . Ale naprawdę się idzie podenerwować przy tej matmie. Szczególnie, że przez pół dnia rozwiązałem jedną stronę zadań, a zostały jeszcze 2.

Damian: Podbijam. Wie ktoś jak w całości rozwiązać to 2. zadanie z mojego pierwszego posta? Nie wiem czemu ramię tego trójkąta wychodzi mi tyle, co powinien mieć duży promień R (koła opisanego na trójkącie). Jak patrzę na różne rysunki, to ramię nie ma prawa być promieniem, bo nie przechodzi przez środek koła. Z drugiej strony wydaje mi się, że ramię z cosinusa na 100% wyliczyłem dobrze. Ech sam już nie wiem .

Kacper: Zapewne wie, tylko dzisiaj taki piękny dzień, że trzeba iść na świeże powietrze Spróbuj ponownie za godzinę i może się uda

Damian: Ok

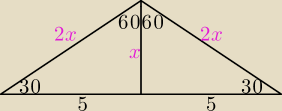Bogdan: Podpowiedź do zadania 2. x√3 = 5

	1		2x*2x*10
Pole P = 5x, P =		(2x + 2x + 10)*r, P =
	2		4*R

Damian: Ha wyliczyłem to, dzięki Bogdan . Z tych wzorów już wcześniej korzystałem, ale wtedy musiałem coś przekręcić i dziwne liczby mi wychodziły. Zaraz jeszcze R wyliczę.

	25√3
P =
	3

	1
P =		(2x + 2x + 10)*r
	2

r = ?

25√3		1		10√3		10√3
	=		(		+		+ 10)*r
3		2		3		3

25√3		1		20√3		10√3
	=		(		+ 10)*r = (		+ 5)*r
3		2		3		3

25√3		10√3*r
	=		+ 5r /:r
3		3

25√3		10√3
	=		+ 5 /:√3
3r		3

25		10		5√3
	=		+		/*3
3r		3		3

25
	= 10 + 5√3 /:5
r

5
	= 2 + √3 /*r
r

5 = 2r + r√3 5 = r(2 + √3)

	5		5		2 − √3		10 − 5√3
r =		=		*		=
	2 + √3		2 + √3		2 − √3		4 − 3

r = 10 − 5√3 = 5(2 − √3)

Damian: Z dużym R mam problem, nie wiem czy obliczyłem to dobrze. W odpowiedzi jest, że powinien

	10√3
wynosić		, czyli tyle ile ramię trójkąta. To jest błąd w odpowiedziach? Mógłby ktoś
	3

potwierdzić, że zastosowany wzór jest odpowiedni do obliczenia promienia koła opisanego na trójkącie, a mój wynik i obliczenia są prawidłowe?

	25√3
P =
	3

	abc
P =
	4R

	10√3
b i c (ramiona) =
	3

a (podstawa) = 10

25√3		10*10√3		10√3
	= (		*		) : (4R)
3		3		3

25√3		1000√3
	= (		) : (4R)
3		9

25√3		250√3
	=		/ *3
3		9R

	250√3
25√3 =		/:25√3
	3R

	10
1 =
	3R

3R = 10 /:3

	10
R =
	3

Damian: Ech zawsze muszę gdzieś błąd popełnić. Nie pomnożyłem √3 z √3. Mało tego, jak sobie to uświadomiłem, to obliczyłem to jako √6 . Nie wiem czemu, ale często jak mam obliczyć 3*3 to piszę wtedy 6. Przy pierwiastkach mam lepiej, bo często zapominam ich pomnożyć. Wynik końcowy jest zgodny z kluczem odpowiedzi. Co prawda długość ramienia trójkąta jest równa długości promienia koła opisanego, co moim zdaniem nie jest możliwe (tak mi się wydaje), ale na pracy klasowej nie będzie mnie to interesować, grunt żeby odpowiedź się zgadzała . Dziękuję wszystkim za pomoc