ekstrema lokalne funkcji
Mia: | | x2 − ax + b | |
Funkcja f(x)= |
| ma w punkcie 3 maksimum lokalne równe 1. Wyznacz a,b oraz |
| | x − 5 | |
pozostałe ekstrema tej funkcji.
Pomocy!
Zaczęłam, ale nie wiem co dalej... (i nie wiem czy to co napisałam jest dobrze...)
Df: R−{5}
| | x2 − 10x + 5a − b | |
f'(x)= |
| |
| | (x−5)2 | |
Df' =R−{5}
f(3)=1
3a − b = 11
10 lis 21:57
Janek191:
oraz
f ' ( 3) = 0
| 9 − 30 + 5 a − b | |
| = 0 |
| ( 3 − 5)2 | |
5 a − b − 21 = 0
−−−−−−
Rozwiązujemy uklad
3 a − b = 11
5 a − b = 21
−−−−−−−−−−−−−−−−−− odejmujemy stronami
2 a = 10
a = 5
====
b = 3 a − 11 = 15 − 11 = 4
====================
zatem
| | x2 − 5 x + 4 | |
f(x) = |
| |
| | x − 5 | |
10 lis 22:15
Janek191:
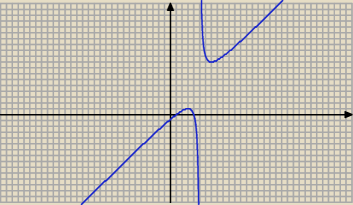
10 lis 22:17
Mia: Dziękuję bardzo! : )
10 lis 22:36
