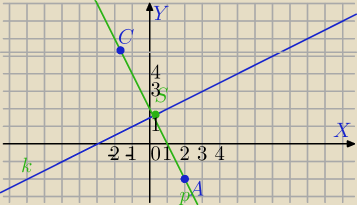
... Hondziarz: Przekątna rombu o polu 9 zawarta jest w prostej x−2y+3=0, a jednym z jego wierzchołków jest punkt A(2,−2). Wyznacz współrzędne pozostałych wierzchołków tego rombu.

Hondziarz:

Mila: P_▱=9 k: x−2y+3=0⇔

	1		3
y=		x+
	2		2

A∉k Przekątne w rombie są prostopadłe i dzielą się na połowy. p⊥K, i A=(2,−2)∊p y=−2x+b i −2=−2*2+b⇔b=2 p: y=−2x+2 S − punkt przecięcia przekątnych

1		3
	x+		=−2x+2
2		2

	1
x=
	5

	8
y=
	5

	1		8
S=(		,		)
	5		5

S jest środkiem AC.

1		2+xc		8		−2+yc
	=		i		=
5		2		5		2

	−8
xc=
	5

	26
yc=
	5

=========

	−8		26
C=(		,		)
	5		5

|AC|*|BD|
	=9
2

|AC|*|BD|=9*2

	−8		26
|AC|=√(		−2)2+(		+2)2 przelicz
	5		5

	18√5
|AC|=
	5

18√5
	*|BD|=9 /*5
5

18√5|BD|=45 /*√5 18*5*|BD|=45√5

	45√5
|BD|=
	18*5

	√5
|BD|=
	2

=========

	√5
|SB|=|SD|=
	4

Dokończysz?.

Hondziarz: x_c i y_c liczysz ze średniej współrzędnych?

Hondziarz:

	√5
Co muszę wykorzystać oprócz |SB|=|SD|=		żeby obliczyć współrzędne B i D
	4

Mila: 1) 18:16 Tak 2) Sposobów jest kilka: Możesz tak: Punkt B leży na prostej k: x−2y+3=0 stąd x=2y−3 B(2y−3,y) wsp. punktu B Teraz z odległości punktów S i B

	√5
|SB|=√(2y−3−(1/5))2+y−(8/5))2=		⇔
	4

	1		√8		√5
(2y−3−(		)2+y−(		)2=(		)2
	5		5		4

Otrzymasz dwa rozwiązania

Hondziarz: to jeszcze wracając do tego zadania. otrzymam dwa rozwiązania i rozumiem, że tylko dwa, czyli, że albo jedno to będzie B albo D lub na odwrót?

Mila: Tak.

Hondziarz: Dzięki Mila

Mila: Dane, kiepsko dobrane i skomplikowały się rachunki. Wyszło Ci zgodnie z odpowiedzią?

daras: w życiu zwykle tak wychodzi, więc po co wygładzać dane?

Eta: "głasanie" jest superr