Zbadaj monotoniczność ciągu o wyrazie ogólnym:
Yolo:
c) a
n = n
2 − 9n − 5
10 lis 14:21
10 lis 14:23
Yolo: ale jeśli wychodzi np: w a)
| | n+4 | | n+3 | |
an+1 − an = |
| − |
| to co dalej? |
| | n+3 | | n+2 | |
10 lis 14:26
J :
wspólny mianownik ..
10 lis 14:26
Yolo: w b) wychodzi mi:
| −4n2 + 10n + 7 | |
| mam liczyć deltę? |
| (n2 + 2n + 2)(n2 + 1) | |
a w c) w odpowiedziach jest że to ciąg niemonotoniczny, dlaczego?
10 lis 15:18
Tadeusz:
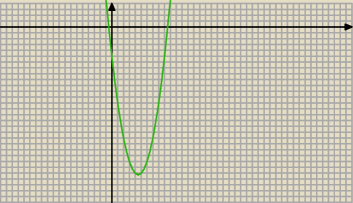
... to zobacz na jakiej krzywej układają się kolejne wyrazy ciągu z c)
10 lis 15:22
Yolo: a w jaki sposób to narysowałeś i skąd brałeś punkty?
| | −4n2 + 10n + 7 | |
i co z podpunktem b) gdzie an+1 − an = |
| ? |
| | (n2 + 2n + 2)(n2 + 1) | |
10 lis 18:07