Sprawdzi nie ktoś Przem: Wyznacz dziedzinę funkcji:

	x−1
f(x)=		D:xeR/{−4}
	x+4

	x2−1
f(x)=		D:xeR/{−2,2}
	x2−4

	x−1
f(x)=		D:xeR/{−4,3}
	(x+4)(x−3

	x2−1
f(x)=		D"xeR/{−5,5}
	x2−25

	x−1
f(x)=		D:xeR/{−√2} Tutaj nie jestem pewien
	x2+4

f(x)=log₂(2x−4) D tej f−cji jest zbiór liczb rzeczywistych większych od 0 czyli D:xe(2,∞) x²+4>0 2x>4 x>2 f(x)=log₃(x−3)+log₃(5−x) D:xe(3,∞) x−3>0 5−x>0 x>0 −x>−5 x>5 f(x)=log_x−1(3−x) D:xe(3,∞) x−1≠0 x−1>0 (3−x)>0 Tego przykładu też nie jestem pewien

Kacper: Co oznacza to D:xe... To jest dziedzina? Jeśli tak to oczywiście źle.

Przem: Tak dziedzina źle to zapisałem

J : 5) źle ... kiedy mianownik się zeruje ? 8) źle ... x−1 > 0 i x − 1 ≠ 1 i 3 − x > 0 ...

Przem: W piątym żadna podstawiona liczba nie da wyniku 0 cokolwiek podstawimy pod potęgę da nam wynik dodatni NIe wiem

Kacper: No to jak żadna nie daje 0, to znaczy, że mogę wstawić dowolną liczbę rzeczywistą

J : ....czyli w 5) ... D = R ...

Przem: Kurcze, faktycznie Poprawiam 8) D:x∊(−∞,1)(3,∞) Dobrze?

Przem:

Przem: f(x)=log(x−2)−√10−x Mam to potraktować jako jedno wyrażenie bo jeśli tak to co z pierwiastkeim zrobic

J : ...warunki: x − 2 > 0 i 10 − x ≥ 0 ...

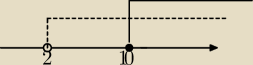
Przem: D:x∊(2,10)u<10,∞) NIe wiem czy dobrze myślę

J : 10 − x ≥ 0 ⇔ x ≤ 10 ...

Przem: Aaa bo zapomniałem że przy dzieleniu przez − odwracamy buźkę. Czyli...

Przem: Będą to wyszyskie liczby rzeczywiste z wykluczeniem 10 Zgłupiałem już

J : ...teraz to zapisz algebraicznie...

J : .... x ∊ (2,10] ...

Przem: x∊(2,10>u<10,∞)

J : .. przecież x ≤ 10..!

Przem: To jeszcze ten przykładzik f(x)=√x²−5 (x−5)(x+5)≥0 x≥√5 x≥−√5 x∊<−√5,√5>u<√5,∞)

Przem: (x−√5)(x+√5)≥0 tak

J : x∊ (−∞,√5> ∪ <√5,+∞)

Przem: Czyli w tym poprzednim zadaniu tylko to jest dziedziną x∊(2,10>

J : ..tak..