Geometria analityczna
O rany julek:
Dwie wersje zadania:
A)łatwiejsza(!?)
Wykaż że prosta o równaniu x−y−4=0 jest dwusieczną kąta przy wierzchołku C
trójkąta o wierzchołkach A(2;−1),B(0;−6),C(6;2)
B)trudniejsza(!?)
Napisz równanie dwusiecznej kąta przy wierzchołku C(danego trójkąta)
[ Odp:x−y−4=0]
10 lis 08:22
razor:
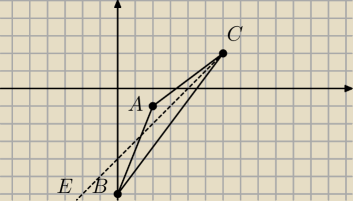
b)
Działamy na wektorach
CA = [2−6, −1−2] = [−4, −3]
CB = [0−6, −6−2] = [−6, −8]
|CA| =
√16+9 = 5
|CB| =
√36+64 = 10
Dzielimy wektor CB na 2 żeby CA i CB miały tę samą długość
|CB|' = [−3,−4]
CA + CB' = [−4−3, −3−4] = [−7, −7]
E = C + [−7, −7] = (6,2) + [−7, −7] = (−1, −5)
Prosta przechodząca przez C i E to dwusieczna kąta C
C(6,2), E(−1,−5)
y = ax+b
6a+b = 2
−a+b = −5
7a = 7
a = 1
b = −4
y = x−4
x−y−4 = 0
10 lis 08:59
Kacper:
Można napisać równania prostej AC i BC, a potem na tej podstawie wyznaczyć równanie
dwusiecznej.

10 lis 09:26
Andriej:
A)
C∊k;x−y−4=0 ,m=1, l⊂CA,m
1=
34 ,n⊂CB,m
2=
43
| |1−34| | | |1−43| | |
| = |
| |
| 1+34*1 | | 1+43*1 | |
B)
| | (xC−xB)2 + (yC−yB)2 | |
( |
| )0,5 =k |
| | (xC−xA)2 + (yC−yA)2 | |
,x
D=(x
C−x
A)(1−k)+x
A∧y
D=(y
C−y
A)(1−k) + y
A,x
D + x
B=2x
E ∧y
D + y
B=2y
E,C,E ∊l=?
10 lis 09:43
Obywatel:
Można opowiadać pierdołki i sofizmaty(vide kacper) ale do czasu i po co
10 lis 09:51
daras: po to żeby tacy jak Obywatel mogli się czepiać
10 lis 10:37
bezendu:
Zaraz sam sobie rozwiąże przecież, więc po co rozwiązywać.
W psychiatryku znowu amnestia ?

10 lis 10:40
Kacper:
Na 11.11 wypuszczają może?

10 lis 10:55
bezendu:
Chyba tak, dostał możliwość powrotu na święto to znowu rozrabia

Ale pewnie ta amnestia tylko
kilkudniowa i panowie z kaftanem zapukają do jego drzwi

10 lis 12:09
 b)
Działamy na wektorach
CA = [2−6, −1−2] = [−4, −3]
CB = [0−6, −6−2] = [−6, −8]
|CA| = √16+9 = 5
|CB| = √36+64 = 10
Dzielimy wektor CB na 2 żeby CA i CB miały tę samą długość
|CB|' = [−3,−4]
CA + CB' = [−4−3, −3−4] = [−7, −7]
E = C + [−7, −7] = (6,2) + [−7, −7] = (−1, −5)
Prosta przechodząca przez C i E to dwusieczna kąta C
C(6,2), E(−1,−5)
y = ax+b
6a+b = 2
−a+b = −5
7a = 7
a = 1
b = −4
y = x−4
x−y−4 = 0
b)
Działamy na wektorach
CA = [2−6, −1−2] = [−4, −3]
CB = [0−6, −6−2] = [−6, −8]
|CA| = √16+9 = 5
|CB| = √36+64 = 10
Dzielimy wektor CB na 2 żeby CA i CB miały tę samą długość
|CB|' = [−3,−4]
CA + CB' = [−4−3, −3−4] = [−7, −7]
E = C + [−7, −7] = (6,2) + [−7, −7] = (−1, −5)
Prosta przechodząca przez C i E to dwusieczna kąta C
C(6,2), E(−1,−5)
y = ax+b
6a+b = 2
−a+b = −5
7a = 7
a = 1
b = −4
y = x−4
x−y−4 = 0



 Ale pewnie ta amnestia tylko
kilkudniowa i panowie z kaftanem zapukają do jego drzwi
Ale pewnie ta amnestia tylko
kilkudniowa i panowie z kaftanem zapukają do jego drzwi 