1.rozwiąż graficznie i algebraicznie nierówność:
arczik: 1.rozwiąż graficznie i algebraicznie nierówność:
c) |x
2+6x+11|<x+7
?(tu nie można kręcić i rozpisywać modułu na dwa coś i coś lub coś?) w jakim przypadku można,
jak liczba po drugiej stronie w nierówności? a jak x to co? płotków (rozpisywania
bezwzględnej) też tu się nie da

2. funkcja f opisana jest wzorem f(x)=−|x
2 −2|x|−3|+2 x∊R
?jak zapisać przekształcenia? bo z resztą sobie poradzę, bo to zadanie z podpunktami ale jak
przekształcenia?
wyjść od: x
2−2x−3 dam moduł na x to będzie na x
2 i x a potem trzeba na f moduł i będzie moduł
w module na x
2 i |x| co ok, ale na x
2 nie potrzebny, nie rozumiem

9 lis 21:58
Eta:
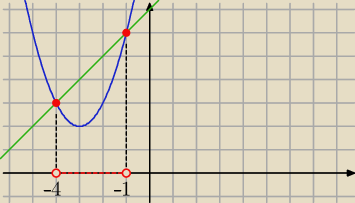
1/
x∊(−4,−1)
9 lis 22:43
arczik: co z rysunku, co dalej?

miałem to rozwiązać
9 lis 23:18
arczik: przenieść prawą na lewą, zredukować przyrównać do większe równe 0 i liczyć deltę? a w innych
przykładach to tak nie działa

9 lis 23:19
Eta:
graficznie ... czyli z rys.
9 lis 23:19
kubuś:
|x2 + 6x + 11| < x + 7, dla x2 + 6x + 11 wyróżnik Δ < 0 czyli x2 + 6x + 11 > 0 dla x∊R
x2 + 6x + 11 − x − 7 < 0
x2 + 5x + 4 < 0
(x + 1)(x + 4) > 0
x∊ (−4, −1)
9 lis 23:27
Eta:
1/ algebraicznie : dla x+7≥0 ⇒ x≥−7
x2+6x+11<x+7 i x2+6x+11> −x−7
x2+5x+4<0 i x2+7x+18>0
x∊(−4,−1) i x∊R i x≥ −7
cz. wspólna:
odp: x∊(−4, −1) ( tak jak na rys
9 lis 23:27
arczik: eta to co napisałeś\aś to jest źle bo nie wiadomo jaki jest x po prawej, nie można tak
rozpisywać, nie w każdym przykładzie tak wyjdzie
10 lis 00:06
Eta:
Napisałam dla x≥−7
10 lis 00:07
 2. funkcja f opisana jest wzorem f(x)=−|x2 −2|x|−3|+2 x∊R
?jak zapisać przekształcenia? bo z resztą sobie poradzę, bo to zadanie z podpunktami ale jak
przekształcenia?
wyjść od: x2−2x−3 dam moduł na x to będzie na x2 i x a potem trzeba na f moduł i będzie moduł
w module na x2 i |x| co ok, ale na x2 nie potrzebny, nie rozumiem
2. funkcja f opisana jest wzorem f(x)=−|x2 −2|x|−3|+2 x∊R
?jak zapisać przekształcenia? bo z resztą sobie poradzę, bo to zadanie z podpunktami ale jak
przekształcenia?
wyjść od: x2−2x−3 dam moduł na x to będzie na x2 i x a potem trzeba na f moduł i będzie moduł
w module na x2 i |x| co ok, ale na x2 nie potrzebny, nie rozumiem 
 1/ x∊(−4,−1)
1/ x∊(−4,−1)
 miałem to rozwiązać
miałem to rozwiązać
