zespolone 2
Kaktus:
Korzystając z interpretacji geometrycznej modułu różnicy liczby zespolonej narysować zbiór
liczb zespolonych spełniających podane warunki
a) |z+i|=3
Czy mogę tak ?
|z−(−i)|=3
koło o promieniu 3 i
środku −i
9 lis 17:58
Mila:
okrąg o środku (0,−1) i r=3
9 lis 18:11
Kaktus:
Czemu o środku (0,−1)
druga współrzędna to wiem ale pierwsza ?
9 lis 18:15
Kaktus:
|2iz+6|≤4
2|iz+3|≤4 /2
|iz+3|≤2
?
9 lis 18:24
Mila:
liczbę z=( −i) mozemy zapisać
z=0−1i, to punkt (0,−1)
9 lis 18:26
Kaktus:
a przykład niżej ?
9 lis 18:30
Kaktus:
okrąg razem z wnętrzem ale o jakim środku
9 lis 18:30
Mila:

cd.18:24
|iz−3i
2|≤2
|i|*|z−3i|≤2⇔
|z−3i|≤2
Albo
|2iz+6|≤4⇔
|2iz−i
2*6|≤4
|2i|*|z−3i|≤4
|z−3i|≤2
9 lis 18:34
Kaktus:
to rozumiem
|zi−3i2|≤2
wyłączam i
|i| |z−3i|≤2
i gdzie się podziało to i teraz ?
|z−3i|≤2 okrąg ale tam jeszcze było |i| ?
9 lis 18:37
Kacper:
i=0+i
|i|=1
9 lis 18:41
Kaktus:

9 lis 18:52
Kaktus:
i2=−1
to skąd ta własność że |i|=1 i i=0+i ?
9 lis 18:55
Kacper:
Jaka własność i=0+i? A definicję modułu liczby zespolonej i jej modułu znasz?
9 lis 19:05
Mila:
√02+12=1
9 lis 19:07
Kaktus:
definicję modułu znam
|z|=√x2+y2
9 lis 20:27
Kaktus:
i jeszcze do pierwszego czy nie powinno być środek (0,−i) r=3
Prawidłowy zapis ?
9 lis 20:40
Mila:
Prawidłowy zapis:
S=(0,−1) wsp. środka okręgu (koła), r=3
9 lis 20:42
9 lis 20:44
Kaktus:
Cały czas mam problem z tą interpretacją
c) 2<|z+2+i|<3
Tutaj będzie pierścień ale znowu nie wiem jak rozpisać
9 lis 20:51
Mila:
2<|z−(−2−i)|<3
S=(−2,−1)
r=2 , R=3
9 lis 20:54
Kaktus:
a nie 0 i coś ?
9 lis 20:58
Kaktus: ?
9 lis 21:04
Mila:
Przeczytaj, to co Ci podałam w linku 20:44.
Postaraj się zrozumieć, co to jest liczba zespolona.
9 lis 21:08
Kaktus:
ok
9 lis 21:11
Kaktus:

|z+5|=|3i−z|
|z+5|=|z−3i|
9 lis 21:32
bezendu:
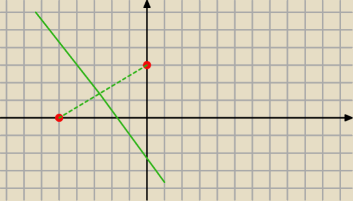
9 lis 21:36
bezendu:
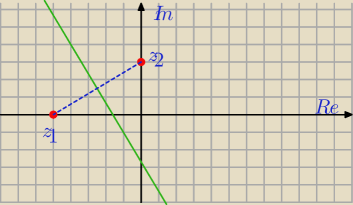
Poprzedni rysunek na szybko był, tutaj ulepszona wersja.
9 lis 21:45
9 lis 22:14
bezendu:
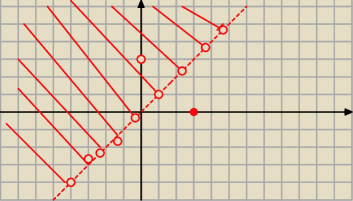
|z−3|>|z−3i|
9 lis 22:27
Kaktus:
Czemu kropka niezamalowana ?
9 lis 22:31
Kaktus: ?
9 lis 22:48
Kaktus: 
?
9 lis 23:05
Kaktus:
:(

9 lis 23:08
Kaktus: ?
9 lis 23:19
Mila:
z−3i≠0 , bo jest w mianowniku ułamka.⇔z≠3i
9 lis 23:56
Kaktus:
Ok, zapamiętam a mogę jeszcze mieć pytanie ? Wiem, że późno już.
10 lis 00:04
Kaktus :
|z+1|+|z−1|=2
10 lis 16:46
Kaktus : ?
10 lis 17:14
Kaktus :
HELP ME
10 lis 18:06
Kaktus :
10 lis 18:20
Mila:
Zaraz, cierpliwości.
Co zrobiłeś w tym zakresie?
10 lis 18:31
Mila:

Zapis |z+1|+|z−1|=2
oznacza ,że suma odległości punktu P(a,b) od punktów A=(−1,0) i B=(1,0) jest równa 2.
Punkty A i B są odległe od siebie o 2, zatem szukany zbiór punktów to odcinek AB.
Albo
Podstaw za z=x+iy i przekształcaj.
10 lis 18:59
Kaktus :
Właśnie nic nie zrobiłem, bo nie bardzo wiem co za figura geometryczna ma to pokazywać.
10 lis 19:15
Mila:
Spróbuj podstawić i ma wyjść odcinek, zobacz, czy nie masz tej informacji w notatkach z
wykładu.
10 lis 19:17
Kaktus :
Na wykładzie miałem tylko macierze i geometrię w R3
10 lis 19:33
Kaktus :
|z+1|≤|z
2+1|
|z+1|≤|z
2−i
2|
|z+1|≤|(z−1)(z+1)|
jak to teraz dokończyć ?
10 lis 19:40
Kaktus : ?
10 lis 20:15
Mila:
Ostatnia linijka źle. |z+1|≤|z−i|*|z+i|
Zaznaczyć na płaszczyźnie zespolonej zbiór ? Tak?
Postać wykładniczą miałeś?
10 lis 20:45
Kaktus :
Nie miałem.
tak zaznaczyć na płasz.
10 lis 20:49
Mila:
Tradycyjnie, to dość skomplikowane rachunki.
W liczniku jest |z+1| czy |z+i|?
10 lis 20:59
Kaktus :
licznik z+i
mianownik z2+1
10 lis 21:06
Mila:
No to co innego. Czy masz odpowiedzi do zadań, jesli tak, to podawaj.
|z+i|≤|z−i|*|z+i|
|z+i|−|z+i|*|z−i|≤0
|z+i|*(1−|z−i|)≤0
|z+i|=0 lub 1−|z−i|≤0
dokończ.
narysuj zbiór, albo opisz.
10 lis 21:17
Kaktus : punkt −i
i pierścień ?
10 lis 21:20
Mila:
A zastrzeżenie co do mianownika dane?
Skąd ten pierścień?
10 lis 21:23
Kaktus :
Czyli ten punkt nie będzie niezamalowane kółeczko
|z−i|<1
okrąg o środku (0,i) i promieniu 1 ?
10 lis 21:48
Mila:
Błędnie zapisałeś nierówność.
1−|z−i|≤0⇔
1≤|z−i|⇔
|z−i|≥1
obszar poza okręgiem o środku (0,1) i promieniu r=1
10 lis 22:20
Kaktus :
Jeszcze jutro wrócę do tego bo w czwartek kolokwium. Dziękuję serdecznie za pomoc.
10 lis 22:22
Mila:

10 lis 22:23
Kaktus:
Polecenie nadal to samo
|ż+2−i|≤|z|
|x−yi+2−i|≤|x+yi|
?
13 lis 19:20
Mila:
licz moduły i do kwadratu.
13 lis 19:37
Kaktus:
√(x+2)2+(y−1)2≤√2 / 2
(x+2)2+(y−1)2≤2
Okrąg o środku (−2,1) i promieniu r=2
13 lis 19:49
J :
..koło wraz z okręgiem ...
13 lis 19:50
razor: od kiedy |z| = √2 ?
√(x+2)2+(y+1)2 ≤ √x2+y2
dokończ
13 lis 19:51
Kaktus:
(x+2)2+(y+1)2≤x2+y2
(x+2)2+(y+1)2≤(x+y)2−2xy
(x+2)2+(y+1)2≤(x+y−√2xy)(x+y+√2xy)
13 lis 19:58
Kaktus: ?
13 lis 20:16
Mila:
(x+2)
2+(y+1)
2≤x
2+y
2
x
2+4x+4+y
2+2y+1≤x
2+y
2
4x+4+2y+1≤0⇔
2y≤−4x−5
13 lis 20:31
Kaktus:
dziękuję a jeszcze wracając do pytania
|z+i|≤|z+i||z−i| czemu nie mogę podzielić przez |z+1|
1≤|z+i|
|z+1|≥1
I czy tutaj nie należy dać założenia z
2+1≠0
z≠i i z≠−i
13 lis 20:37
Kaktus: ?
13 lis 21:34
Mila:
Założenie trzeba dać, to oczywiste.
Gubisz rozwiązanie przez takie dzielenie , a poza tym to gdzie widzisz |z+1|i skąd ten wynik
1≤|z+i|.
13 lis 21:41
Kaktus:
ok, już zaczynam rozumieć to wszystko

najgorsze przede mną
13 lis 21:43
Mila:
Ciągle mylisz liczbę i z liczbą 1 .
13 lis 21:45
Kaktus:
wiem

13 lis 21:48
Kaktus:
3|z−1|<|z2−1|<6|z+1|
a takie coś ?
3|z−1|<|z−i||z+i|≤6|z+1|
13 lis 22:17
Mila:
z2−1=(z−1)*(z+1) natomiast z2−i2=(z−i)*(z+i) to o co w końcu chodzi?
Rozpisz na dwie nierówności i rozwiąż układ nierówności.
13 lis 22:23
Kaktus:
po prostu rozpisałem |z2−1| a |z2−i2| ale to jest raczej źle bo winno być |z2+i2|
3|z−1|<|z−i||z+i|<6|z+1|
13 lis 22:32
Mila:
Napisz oryginalną treść zadania .
13 lis 22:34
Kaktus:
Na płaszczyźnie zespolonej narysuj
3|z−1|≤|z2−1|≤6|z+1|
13 lis 22:51
Mila:
To napisz mój niebieski wzór i koniunkcję nierówności.
13 lis 23:09
Kaktus:
z2−1
z2+i2
13 lis 23:11
Mila:
Po co? Przecież z2+i2 to suma kwadratów, a potrzebna różnica kwadratów, wszystko zapomniałeś,
za dużo uczysz się.
1=12
|z2−1|=|z2−12|=|(z−1)*(z+1)|
13 lis 23:14
Kaktus:
Faktycznie !
3|z−1|≤|z−1|z+1|≤6|z+1|
13 lis 23:15
Mila:
Dalej.
13 lis 23:16
Kaktus:
3|z−1|−|z−1||z+1|≤6|z+1|
|z−1(|3−|z+1|)≤6|z+1|
i teraz nie wiem
|z−1| czyli punkt 1,0
13 lis 23:22
Mila:
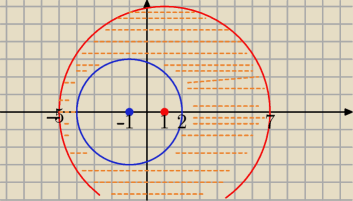
3|z−1|≤|z−1|*|z+1|≤6|z+1|⇔
3|z−1|≤|z−1|*|z+1| i |z−1|*|z+1|≤6|z+1|
(3|z−1|−|z−1|*|z+1| ≤0) i (|z−1|*|z+1|−6|z+1|≤0 )
(|z−1|*(3−|z+1|)≤0 i (|z+1|*(|z−1|−6)≤0 )
|z−1|=0 lub 3≤|z+1|) i |z+1|=0 lub |z−1|≤6
dokończ
13 lis 23:44
Mila:
Dobranoc

13 lis 23:57
Kaktus:
Dobranoc. ale już tutaj wszystko jest skończone

14 lis 00:05
 cd.18:24
|iz−3i2|≤2
|i|*|z−3i|≤2⇔
|z−3i|≤2
Albo
|2iz+6|≤4⇔
|2iz−i2*6|≤4
|2i|*|z−3i|≤4
|z−3i|≤2
cd.18:24
|iz−3i2|≤2
|i|*|z−3i|≤2⇔
|z−3i|≤2
Albo
|2iz+6|≤4⇔
|2iz−i2*6|≤4
|2i|*|z−3i|≤4
|z−3i|≤2

 |z+5|=|3i−z|
|z+5|=|z−3i|
|z+5|=|3i−z|
|z+5|=|z−3i|

 Poprzedni rysunek na szybko był, tutaj ulepszona wersja.
Poprzedni rysunek na szybko był, tutaj ulepszona wersja.

 ?
?

 Zapis |z+1|+|z−1|=2
oznacza ,że suma odległości punktu P(a,b) od punktów A=(−1,0) i B=(1,0) jest równa 2.
Punkty A i B są odległe od siebie o 2, zatem szukany zbiór punktów to odcinek AB.
Albo
Podstaw za z=x+iy i przekształcaj.
Zapis |z+1|+|z−1|=2
oznacza ,że suma odległości punktu P(a,b) od punktów A=(−1,0) i B=(1,0) jest równa 2.
Punkty A i B są odległe od siebie o 2, zatem szukany zbiór punktów to odcinek AB.
Albo
Podstaw za z=x+iy i przekształcaj.

 najgorsze przede mną
najgorsze przede mną

 3|z−1|≤|z−1|*|z+1|≤6|z+1|⇔
3|z−1|≤|z−1|*|z+1| i |z−1|*|z+1|≤6|z+1|
(3|z−1|−|z−1|*|z+1| ≤0) i (|z−1|*|z+1|−6|z+1|≤0 )
(|z−1|*(3−|z+1|)≤0 i (|z+1|*(|z−1|−6)≤0 )
|z−1|=0 lub 3≤|z+1|) i |z+1|=0 lub |z−1|≤6
dokończ
3|z−1|≤|z−1|*|z+1|≤6|z+1|⇔
3|z−1|≤|z−1|*|z+1| i |z−1|*|z+1|≤6|z+1|
(3|z−1|−|z−1|*|z+1| ≤0) i (|z−1|*|z+1|−6|z+1|≤0 )
(|z−1|*(3−|z+1|)≤0 i (|z+1|*(|z−1|−6)≤0 )
|z−1|=0 lub 3≤|z+1|) i |z+1|=0 lub |z−1|≤6
dokończ

