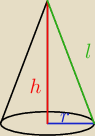
Granica funkcji Rouqi: Niech S(h) oznacza powierzchnię całkowitą stożka o ustalonej podstawie r i wysokości h. Znajdź granicę S(h) za pomocą: a) rozumowania geometrycznego b) obliczeń Z tw Pitagora : l² = h² + r² ⇒ l = √h² + r² S = Pp + Pb Pp = πr² Pb = πrl ⇒Pb = πr√h² + r² jak znaleźć w takim zadaniu granicę za pomocą rozumowania geometrycznego i obliczeń?

Rouqi: ktoś umie pomóc w tym zadaniu

Gray: Granicę przy h→? Do 0?

Rouqi: nie rozumiem

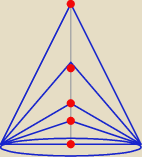
Gray: Zakładam, że chodzi o h→0. Z interpretacji geometrycznej widać, że jak h→0 to stożek coraz bardziej kładzie się na podstawę: pole jego powierzchni bocznej coraz bliższe jest polu podstawy. W granicy pokrywa się z polem podstawy, skąd S(h) → 2Pp = 2πr². To samo otrzymamy z obliczeń: S(h) = Pp+Pb = πr² + πr√h²+r² → πr² + πr√r² = 2πr².

Gray: Napisałeś (−łaś): "...Znajdź granicę S(h) ...." więc pytam, granicę jaką? Do czego ma zmierzać h? Założyłem, że h→0.

Rouqi: w tym zadaniu właśnie nie jest dokąd te h ma zmierzać

=:=: h→0

Rouqi: można w sumie na 2 przypadki w zasadzie w takim zadaniu to rozważyć gdy h → ∞ i h→ 0 tak?

=:=:

Rouqi: czyli jeżeli chodzi o granicę to h musi dążyć do 0 tak?

Rouqi:

Rouqi:

Rouqi:

Rouqi: