parametr Aguella: Dla jakich wartości patametru m istnieją dwa różne rozwiazania x1 i x2 równania (2m−3)x² +4mx+m−1=0 błagam ludzie opis

pigor: ..., np. tak: masz równanie z parametrem m dane wzorem (2m−3)x²+4mx+m−1=0, czyli postaci ax²+bx+c=0, które ma (o ile istnieją) dwa różne rozwiązania x₁≠x₂ rzeczywiste ⇔ a≠0 i Δ>0 ⇔ a=2m−3≠0 i b²−4ac=(4m)²−4*(2m−3)(m−1) >0 ⇔ ⇔ 2m≠3 /:2 i 16m²−4(2m²−2m−3m+3) >0 /:4 ⇔ ⇔ (*) m≠³₂ i 4m²− (2m²−5m+3) >0 ⇒ 4m²− 2m²+5m−3 >0 ⇔ ⇔ 2m²+5m−3 >0 i tu możesz te nierówność rozwiązać "deltą" lub dalej np. tak: ⇔ 2m²−m+6m−3 >0 ⇔ m(2m−1)+3(2m−1) >0 ⇔ ⇔ (2m−1)(m+3) >0 /:2 ⇔ (m−¹₂)(m+3) >0 , to stąd i z (*) ⇔ (m<−3 v m>¹₂) i m≠³₂ ⇔ m<−3 v ¹₂< m<³₂ v m>³₂ ⇔ ⇔ m∊(−∞;−3) U (¹₂; ³₂) U (³₂;+∞) . ...

Aguella: troche się pogubiłam− można to bardziej po kolei ?

pigor: ..., , chyba żartujesz, ja swoje zrobiłem; dobranoc ...

Aguella: tylko fajnie że dalej nie rozumiem− za dużo skrótów myślowych jak dla mnie dobra... i tak dzięki

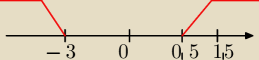Metis: Rozpoczynamy od odpowiednich założeń: a≠0 inaczej otrzymalibyśmy równanie liniowe ( a tego nie chcemy )Twój współczynnik a to współczynnik stojący przy x² czyli : 2m−3 stąd: 2m−3≠0⇔2m≠3⇔ m≠1,5 Zakładamy również że x1≠x2, z treści zadania ( dwa różne rozwiazania) Mamy odpowiednie założenie , przejdźmy do rozwiązania: Rozwiązanie : Funkcja kwadratowa ma dwa różne rozwiązania, czyli dwa różnie pierwiastki wtedy gdy Δ>0 Δ=b²−4ac , stąd podstawiając odpowiednie wyrazy [a=2m−3, b=4m, c=m−1] otrzymujemy : (4m)²−4*(2m−3)(m−1) Otrzymujemy nierówność która należy rozwiązać: Δ>0 (4m)²−4*(2m−3)(m−1) >0 Po uproszczeniach otrzymujemy 2m²+5m−3 >0 , gdzie m≠1,5 Rozwiązując powyższą nierówność otrzymujemy przedział: x>0,5 x<−3 (Czerwony przedział) Widzisz, że zawiera się w nim 1,5. Zatem musimy "wywalić" go z przedziału , otrzymujemy:

	1		3		3
m∊(−∞,−3) U (		,		) U (		, +∞)
	2		2		2

Czyli to samo co u pigora