ekstrema i przedziały monotonicznosci funkcji kacper: Wyznaczyć ekstrema i przedziały monotoniczności funkcji

	x
f(x)=
	lnx

Umiem jedynie wyliczyć z tego pochodną i wychodzi mi:

	lnx−1
f'(x)=
	(lnx)2

Bardzo proszę o pomoc w rozwiazaniu...

J : ..teraz warunek konieczny ... kiedy ta pochodna się zeruje... ?

kacper: gdy lnx−1=0 ? A co z dziedziną funkcji i pochodnej? Jaka powinna być?

J : ...dziedzina: x > 0 i lnx ≠ 0 ... ustal..

kacper: Hmm czyli to tak powinno być? Df=(x,+∞) Df'=Df f'(x)=0 <=> lnx−1=0 lnx=1 x^lnx=e{1} x=1 Zatem: f rośnie dla x∊(1,+∞) f maleje dla x ∊ (0,1) f_min=1

	1
f(1)=		=0
	ln1

tak?

J : zacznijmy od dziedziny... co ty za bzdury wypisujesz ... kiedy lnx = 0 ...?

kacper: Nie rozumiem Z mianownika wiadomo, że x>0 a kiedy lnx = 0 nie wiem...

J : x > 0 ... bo to liczba logarytmowana .. lnx= 0 ⇔ x = 1 ... i teraz ustal dziedzinę...

kacper: W takim razie dziedziną funckji jest D:x∊(0,1) suma (1,+∞) tak?

J : OK ..teraz warunek konieczny ... f'(x) = 0

kacper: Czyli

	lnx−1
f'(x)=
	(lnx)2

Czyli wychodzi, że mianownik jest zawsze większy od zera więc patrzę tylko na licznik? f'(x)=0 wtedy i tylko wtedy, gdy lnx−1=0 tak? lnx=1 e^lnx=e¹ x=1

J : źle ... lnx = 1 ⇔ lnx = lne ⇔ x = e ..

kacper: Faktycznie... I co dalej należy policzyć? Zwykle teraz rysowałem na osi dziedzinę i to co wyszło z warunku koniecznego f'(x)=0. ale jak narysować to "e"?

J : .teraz trzeba zbadać, czy pochodna zmienia znak w punkcie x = e ... zauważ,że mianownik jest zawsze dodatni... trzeba zbadać znak licznika.. g(x) = lnx − 1 .... zbadaj czy zmienia znak w puncie x = e...

J :

	x
...dobra ...g(x) = lnx − 1 = lnx − lne = ln		.... i teraz się zastanów, czy zmienia znak
	e

w x =e

J :

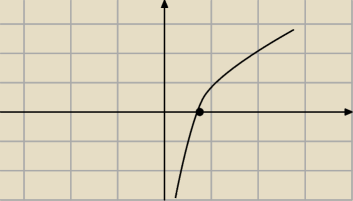
	x		x
..to jest wykres g(x) = ln		... przecina oś OX w punkcie (1,0) czyli		= 1
	e		e

kacper: Dziękuję za pomoc...

daras: http://www.wolframalpha.com/input/?i=x%2Flnx&lk=4