??? ???: Potrzebuje pomocy z tą funkcją y=x³−x²−x+1. Muszę narysować wykres i określić własności. Nie prosze o rozwiązanie tylko o jakieś podpowiedzi z góry dzięki.

wmboczek: wyznacz P charakterystyczne − przecięcia z osiami i maksima/minima lokalne (z pochodnej) i połącz wężykiem

???: Nie mam pojęcia jak to zrobić Czy wyznaczenie miejsc zerowych nie bylo by prostsze ?

???: Nie przypominam sobie żebym miał o pochodnych nie da się tego w inny sposób rozwiązać?

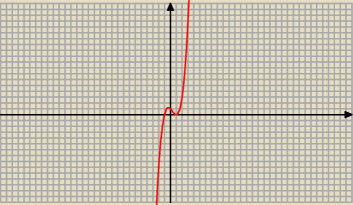
Janek191: y = x³ − x² − x + 1 = x² *(x − 1) − ( x −1) =( x − 1)*( x² −1) = ( x − 1)*(x − 1)*(x + 1) Miejsca zerowe: x = 1 i x = − 1 Dla x = 0 jest y = 0 − 0 − 0 + 1 = 1 Dla x = −2 jest y = − 8 − 4 + 2 + 1 = − 9 Dla x = 2 jest y = 8 − 4 − 2 + 1 = 3 Dla x = 3 jest y = 27 − 9 − 3 + 1 = 16

Gruszka: Jeżeli potrzebujesz opisu potrzebnego do narysowania takiej funkcji, to nikt nie uzna Ci takich pojedynczych obliczeń. Zawsze zaczynaj sobie od: 1)Dziedzina (to jest bardzo ważne), w twoim przypadku x∊R 2)Przecięcia z OX: y=0 x3−x2−x+1=0 x²(x−1)−(x−1)=0 (x²−1)(x−1)=0 x=1 x=−1 Przecięcie z OY: x=0 ⇔f(x)=1 P(0,1) 3) Musisz obliczyć asymptoty, w tym przypadku tylko poziome, ponieważ x∊R, także pionowe nie istnieją. lim = x3−x2−x+1=lim = x³(1−1/x−1/x²+1/x³)=∞ x→∞ x→∞ lim = x3−x2−x+1=lim = x³(1−1/x−1/x²+1/x³)=−∞ x→−∞ x→−∞ Wniosek: Brak asymptot pionowych i poziomych funkcji! 4) Musisz obliczyć pochodną: f'(x)=3x²−2x−1 Df'(x)=Df(x) 5) Warunek konieczny ⇔ f'(x)=0 3x²−2x−1=0 Δ=4+12=16 x1=2−4/6= −1/3 x2=2+4/6=1 Warunek wystarczający: Musisz sobie narysować funkcję f"(x) i odczytać ekstrema. Otrzymasz, że xmax=−1/3 ymax(x)=32/27 xmin=1 ymin(x)=0 Określamy teraz: f"(x) ≥0, czyli f(x) jest rosnąca w przedziałach: (−∞,−1/3>, <1,∞) f"(x) ≤0, czyli f(x) jest malejąca w przedziale: <−1/3,1> Masz już wszystko czego potrzebujesz, teraz musisz sporządzić tabelkę, muszą znaleźć się w niej przedziały monotoniczności, wszystkie rozwiązanie (x) oraz ich wartości (y). Sporządź tabelkę dla pochodnej i dla funkcji, będzie Ci łatwiej. Na koniec pamiętaj, że rysujesz funkcję.