równanie ogólne prostej astrolog: Witam, zmagam się z takim zadaniem: W prostokącie ABCD dane są: wierzchołek C(2,4) i wektor AB = [4,4]. Wyznacz równanie ogólne prostej zawierającej przekątną AC tego prostokąta, jeśli wiadomo, że wierzchołek A należy do prostej k: x − y −4 =0. z góry dziękuję za pomoc

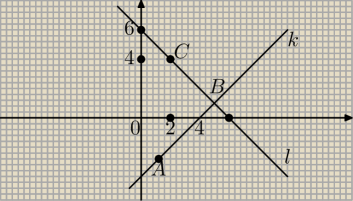
Tereska: wektor AB=[4,4] oznacza, że zawiera się on w prostej o równaniu y=x+b, więc wierzchołki A i B leżą na prostej o takim równaniu. Z treści zadania A należy do prostej k: x−y−4=0, równanie kierunkowe tej prostej to y=x−4 i jest to prosta o r−niu y=x+b gdzie b=−4 Zatem A i B leżą na prostej k: y=x−4 Prostopadła do k l: y=−x+b i przechodząca przez C 4=−2+b b=6 ma równanie kierunkowe y=−x+6 Na przecięciu prostych k i l leży punkt B, więc rozwiązaniem układu równań: 1. y=x−4 2. y=−x+6 są współrzędne wierzchołka B dodajemy stronami 2y=2 y=1 po np. podstawieniu do 2. x=5 B(5,1) Współrzędne wierzchołka A: Wektor AB=[4,4]=[x_b−x_a,y_b−y_a] [4,4]=[5−x_a,1−y_a] 4=5−x_a 4=1−y_a x_a=1 y_a=−3 A(1,−3) Równanie prostej przechodzącej przez A i C: y−y_a =( (y_c−y_a)/(x_c−x_a)) *(x−x_a) po podstawieniu współrzędnych y+3=⁴⁺³₂₋₁*(x−1) y+3=7x−7 więc równanie ogólne szukanej prostej: y−7x+10

astrolog: Dzieki