dziedzina funkcji
Geber: Dziedziną funkcji f(x)=log2x−1x może być zbiór:
a) (−∞,0) (1,+∞)
b) (0,1)
c) ( −1,+∞)
d) (1,+∞)
7 lis 15:24
J :
a)
7 lis 15:25
Geber: hmmm a>1 więc dziedziną są liczby R+ rozważałam b lub d?
7 lis 15:29
J :
| | x−1 | |
warunek: |
| > 0 ⇔ (x−1)*x > 0 ... i sprawdź ... |
| | x | |
7 lis 15:30
Geber: no tak i wyszło mi że x∊(−∞,−1)∪(0,+∞) a z własności funkcji logarytmicznej o podstawie a > 1:
Dziedzina: D = R+. więc?
7 lis 15:33
Geber: no tak i wyszło mi że x∊(−∞,−1)∪(0,+∞) a z własności funkcji logarytmicznej o podstawie a > 1:
Dziedzina: D = R+. więc?
7 lis 15:33
J :
bez względu na podstawę, liczba logarytmowana musi być dodatnia...
7 lis 15:35
J :
... źle Ci wyszło ... ma Ci wyjść odpowiedź a)
7 lis 15:36
Geber: ok
7 lis 15:37
Geber: to coś powaliłam
7 lis 15:37
J :
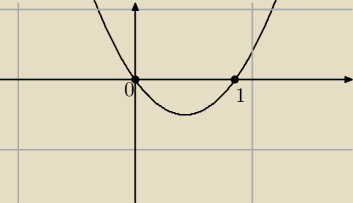
..popatrz na wykres..
7 lis 15:40
Geber: no tak w najprostszym miejscu...przepisałam x(x+1) zamiast x(x−1)
dzięki
7 lis 15:44