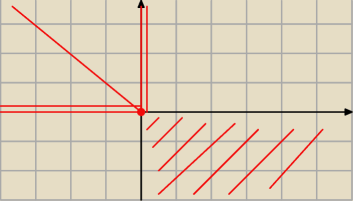
Geometria analityczna olkaq: Hej, sprawdzi ktoś czy dobrze narysowałam? Zaznacz w układzie współrzędnych zbiór punktów, których współrzędne (x,y) spełniają równanie: x−|x| = y+|y|

PW: Dla x<0 i y>0 równanie przyjmuje postać 2x = 2y y = x − takich punktów, dla których x i y są różnych znaków i jednocześnie x=y po prostu nie ma. Dla x < 0 i y < 0 równanie ma postać 2x = 0 x=0 − takich par, dla których x < 0 i jednocześnie x = 0 też nie ma. Dla x = 0 równanie przyjmuje postać 0 = y + |y| i jest spełnione, gdy |y| = − y, to znaczy dla y < 0 − należy zaznaczyć ujemną półoś igreków. Dla y = 0 równanie ma postać x − |x| = 0, czyli jest spełnione dla x ≥ 0 − należy zaznaczyć pary (x, 0) dla x≥0, czyli nieujemną półoś iksów.