| 1 | 2 | ||
= | |||
| 2 | a |
 zad. 1.
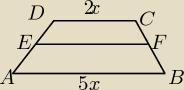
Mam trapez ABCD, gdzie:
|AB| = 5x − dłuższa podstawa trapezu
|DC| = 2x − krótsza podstawa trapezu
|EF| = długość odcinka łączącego środki ramion tego trapezu
5x − 2x = 9
3x = 9 / :3
x = 3. z tego wynika, że długość boku |DC| = 6, bo 2*3 = 6 oraz długość boku |AB| = 15, bo 5*3
= 15.
Teraz obliczam długość odcinka |EF|, a wiemy, że długość odcinka łączącego środki ramion tego
trapezu (|EF|), to suma podstaw tego trapezu podzielona przez 2.
i mam:
|EF| = ( |DC| + |AB| ) : 2 = ( 6 + 15 ) : 2 = 21 : 2 = 10,5
Odp. Długość odcinka łączącego środki ramion tego trapezu ( |EF| ) wynosi 10,5.
zad. 1.
Mam trapez ABCD, gdzie:
|AB| = 5x − dłuższa podstawa trapezu
|DC| = 2x − krótsza podstawa trapezu
|EF| = długość odcinka łączącego środki ramion tego trapezu
5x − 2x = 9
3x = 9 / :3
x = 3. z tego wynika, że długość boku |DC| = 6, bo 2*3 = 6 oraz długość boku |AB| = 15, bo 5*3
= 15.
Teraz obliczam długość odcinka |EF|, a wiemy, że długość odcinka łączącego środki ramion tego
trapezu (|EF|), to suma podstaw tego trapezu podzielona przez 2.
i mam:
|EF| = ( |DC| + |AB| ) : 2 = ( 6 + 15 ) : 2 = 21 : 2 = 10,5
Odp. Długość odcinka łączącego środki ramion tego trapezu ( |EF| ) wynosi 10,5.
 zad. 1.
Mam trapez ABCD, gdzie:
|AB| = 5x − dłuższa podstawa trapezu
|DC| = 2x − krótsza podstawa trapezu
|EF| = długość odcinka łączącego środki ramion tego trapezu
5x − 2x = 9
3x = 9 / :3
x = 3. z tego wynika, że długość boku |DC| = 6, bo 2*3 = 6 oraz długość boku |AB| = 15, bo 5*3
= 15.
Teraz obliczam długość odcinka |EF|, a wiemy, że długość odcinka łączącego środki ramion tego
trapezu (|EF|), to suma podstaw tego trapezu podzielona przez 2.
i mam:
|EF| = ( |DC| + |AB| ) : 2 = ( 6 + 15 ) : 2 = 21 : 2 = 10,5
Odp. Długość odcinka łączącego środki ramion tego trapezu ( |EF| ) wynosi 10,5.
zad. 1.
Mam trapez ABCD, gdzie:
|AB| = 5x − dłuższa podstawa trapezu
|DC| = 2x − krótsza podstawa trapezu
|EF| = długość odcinka łączącego środki ramion tego trapezu
5x − 2x = 9
3x = 9 / :3
x = 3. z tego wynika, że długość boku |DC| = 6, bo 2*3 = 6 oraz długość boku |AB| = 15, bo 5*3
= 15.
Teraz obliczam długość odcinka |EF|, a wiemy, że długość odcinka łączącego środki ramion tego
trapezu (|EF|), to suma podstaw tego trapezu podzielona przez 2.
i mam:
|EF| = ( |DC| + |AB| ) : 2 = ( 6 + 15 ) : 2 = 21 : 2 = 10,5
Odp. Długość odcinka łączącego środki ramion tego trapezu ( |EF| ) wynosi 10,5.

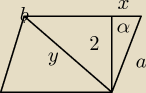 α=30o
bok można obliczyć z sin
α=30o
bok można obliczyć z sin
| 2 | ||
sinα= | ||
| a |
| 2 | ||||||||
a= | =4
| |||||||
|