proszę o wytłumaczenie ;): może mi ktoś coś wytłumaczyć mam takie zadanie: 2cos²x − cosx = 1 i skorzystałam tutaj z delty, wyszło mi: cosx = − 1/2 cosx = 1

	2		1
i teraz już poległam jak mam cosx = −1/2 to wiem, że x =		π + 2kπ lub		π +
	3		3

2kπ a jak będzie z tą jedynką? muszę to znaleść na wykresie

;): aha i jeszcze mam, że t ∊ < −1, 1> i powiedzcie czy to chodzi o oś y

Godzio: w tym pierwszym to

	2		2
x=		π+2kπ v x=−		π+2kπ
	3		3

cosx=1 x=0+2kπ −> x=2kπ

;):

	2		1
nie zgadzam się z tym pierwszym... ma być x =		π + 2kπ lub x =		π + 2kπ. Ja tak
	3		3

przynajmniej uważam i tak było na lekcji

Godzio: napewno nie cosx x=x₀+2kπ v x=−x₀+2kπ

	2
tu naszym x0 jest		π, jesteś pewien dalej ?
	3

Godzio: dokładnie to tak sie rozpisuje: cosx=a a∊(−1,0)∪(0,1) x₀=... x=x₀+2kπ v x=−x₀+2kπ

Godzio: dokładnie to tak sie rozpisuje: cosx=a a∊(−1,0)∪(0,1) x₀=... x=x₀+2kπ v x=−x₀+2kπ

;): no tak mam w zeszycie jak napisałam

	2		1		1
π −		π =		π i stąd x =		π + 2kπ
	3		3		3

;): a ten przedział co podałam dotyczy osi x

Piotr:

	1
y bo x podaje sie w radianach czyli π		π itd
	2

a to co ty masz napisane to dobrze tyle ze do sin i w takim wypadku : x₀+2kπ v π−x₀+2kπ

	2		2
podstawiajac x0 do drugiego otrzymalibysmy π−(−		π) co daje nam π+		π
	3		3

Godzio: u sin tak jest a ten przedział to do y sie tyczy sinx=a a∊(−1,0)∪(0,1) x=x₀+2kπ v x=π−x₀+2kπ

Godzio: widze że ktos mnie już uprzedził

;): nie rozumiem to co ja napisałam jest dobrze tak mam zapisane w zeszycie z lekcji

;):

	2
skąd się wzięło −		π tam było na plusie
	3

;):

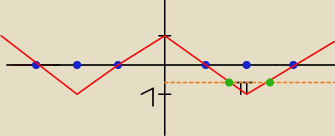
	2
te pkt na zielono mnie interesują, pierwszy to		a drugi wg Was ile ma
	3