funkcja wypukła i odwrotna dronguu: Mam problem z zadaniami z funkcji wypukłej oraz z funkcją odwrotną. 1. Wykazać, że g(x)= √2^x−1 jest wypukła. 2. Znajdź funkcję odwrotną do y= 1−x/1+x 3. Znależć funkcję odwrotną y=log₃x Mój znakomity profesor zaczął robić to zadanie tak: log₃(αx+ βy) ^{(αx βy−2)} ≤ log₃.. Niestety nie miałam jeszcze przyjemności poznać pochodnej, wiec byłabym wdzieczna za pomoc.

PW: Zadanie 3. to jakieś nieporozumienie − to raczej nie anegdota o roztargnionym profesorze, ale anegdota o studencie, który nie wie co do czego przytknąć.

dronguu: uwierz mi że zrozumienie mojego profesora na cwiczeniach jest trudne. zwłaszcza iż nie jest on z polski. jezeli zas jestes taki cwany to czemu nie pokazesz co potrafisz.

Janek191: z.2

	1 − x
y =
	1 + x

1 − x = y*( 1 + x) 1 − x = y + x*y 1 − y = x + x*y x*( 1 + y) = 1 − y

	1 − y
x =
	1 + y

Po zamianie zmiennych otrzymamy

	1 − x
y =		− funkcja odwrotna
	1 + x

================

Janek191: z. 3 y = log₃ x ; x > 0 y = log₃ x ⇔ x = 3^y Po zamianie zmiennych mamy y = 3^x − funkcja odwrotna ======

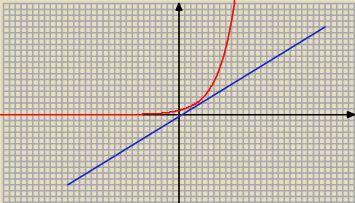
Janek191: y = √2^{x − 1} Na wykresie widać, że jest to funkcja wypukła − jest położona nad każdą jej styczną w dowolnym punkcie P = ( x_o; f(x_o) )

PW: Droga dronguu, pozwolę sobie zacytować: jezeli zas jestes taki cwany to czemu nie pokazesz co potrafisz. i odpowiedzieć: − O wpół do drugiej w nocy nie zajmuję się pokazywaniem znanego ze szkoły średniej faktu, że funkcja logarytmiczna jest odwrotna do wykładniczej. To nawet wstyd, żeby student o to pytał.

dronguu: drogi PW. to że funkcja logarytmiczna jest odwrotna do wykładniczej doskonale wiem, Gdybyś sie dokładniej przyjrzał chodziło mi o sposób w jaki moj profesor kazał wykonać nam to zadanie. wstyd? Znane jest powiedzenie, iż kto pyta nie błądzi. Raczej wole dowiedzieć sie jak to zadanie mogą wykonać inni bo nie ma tylko jednej metody na wszystko. Nie każdzy jest geniuszem w każdej dziedzinie. To ile czasu spedzam na nauke to raczej moja sprawa, wiec byłoby mi strasznie miło gdybyś zostawił temat w spokoju, poszedł dalej, a nie komentował styl życia innych bo od tego raczej nie jest ta strona powodzenia w dalszym sympatycznym i serdecznym dla innych życiu!