Funkcja kwadratowa dyzio: Wyznacz współczynniki a, b, c we wzorze funkcji kwadratowej, wiedząc, że do wykresu tej funkcji należą punkty A(−2 ; −10) B(4 ; −10) C(1 , 2). Proszę o pomoc.

Piotr: uklad 3 rownan z 3 niewiadomymi i jedziesz

dyzio: −10 = 4a ² − 2b + c −10 = 16a² + 4b + c 2 = 4a² + 4b + c tak ?

Piotr: a skad a² ? zapisz tak : pkt A : 4a − 2b + c = −10

dyzio: Rzeczywiście 4a − 2b + c = −10 16a + 4b + c = −10 a + b + c = 2 i teraz np. c = −10 − 4a + 2b i podstawiam do drugiego ?

dyzio: odpowie ktoś ?

dyzio: ?

bezendu: Wyznacznikami policz.

dyzio: za bardzo nie wiem jak bo to 3 równania są... metodą podstawiania mi coś nie wychodzi

Mila: 4a − 2b + c = −10 16a + 4b + c = −10 a + b + c = 2 Od drugiego odejmuje pierwsze, od drugiego odejmuję trzecie 12a+6b=0 15a+3b=−12 teraz licz dalej sam

dyzio: b = −2a 15a − 6a = −12 9a = − 12

	12
a = −
	9

	1
a = − 1
	3

Dzięki za pomoc dalej sobie poradzę

ICSP: zauważmy, ze f(−2) = f(4) oraz f(1) = 2 skąd : f(x) = a(x−1)² + 2 Wstawiając współrzędne jednego z punktów A i B doliczysz współczynnik a. Zamiast działać schematami postaraj się myśleć, a znacznie uprościsz sobie życie

Mila:

	4
a=−
	3

	8
b=
	3

	2
c=
	3

	4		8		2
f(x)=−		x2+		x+
	3		3		3

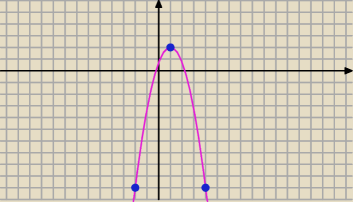
II sposób Punkty (−2,−10), (4,−10) są symetryczne względem prostej x=1, ⇔na tej prostej leży wierzchołek paraboli, właśnie mamy dany (1,2) p=1, q=2 f(x)=a*(x−1)²+2 f(4)=−10 a*(4−1)²+2=−10 9a=−12

	−12		−4
a=		=
	9		3

	−4
f(x)=		(x−1)2+2 postać kanoniczna ,
	3

po podniesieniu otrzymasz wzór w postaci ogólnej.