Rozwiąż nierówności wymierne Maciej: Rozwiąż nierówność: 2^x+1 ≤ 2* √3*2^x+4 mógłby mi ktoś doradzić co z tym zrobić? próbowałem to pomnożyć stronami przez ( )² ale nie wyszło mi coś

Janek191: Podnosimy obustronnie do kwadratu ( obie strony są dodatnie )

Maciej: 4^x+1 ≤ 4 * 3*2^x+4

Janek191: Brakuje nawiasu po prawej stronie i zamień 4 na 2²

Maciej: 4^x * 4 ≤ 4 * 3 * 2^x + 4 2^2x * 4 ≤ 12 2^x + 4 2^x = t, gdzie t > 0 4t² ≤ 12t + 4 4t² − 12t − 4 ≤ 0 co ja tu źle robię?

Maciej: znaczy tak? 4^x+1 ≤ 2(3*2^x+4) 2^2x+2 ≤ 2(3*2^x+2²) i co dalej powinienem zrobić z tą 2 przy nawiasie?

Janek191: Powinno być : ( 2^{x + 1})² ≤ 4*( 3*2^x + 4)

Janek191: 2^{2x + 2} ≤ 12*2^x + 16 2² *(2^x)² − 12*2^x − 16 ≤ 0 / : 4

Janek191: (2^x)² − 3*2^x − 4 ≤ 0 2^x = t > 0 t² − 3 t − 4 ≤ 0

Maciej: Δ=9+16=25 √Δ = 5

	3−5
t1=		= −1 sprzeczne z założeniem
	2

	3+5
t2=		= 4
	2

jak mam teraz to dalej obliczać? bo t₁ sprzeczne z założeniem więc chyba paraboli już nie narysuję?

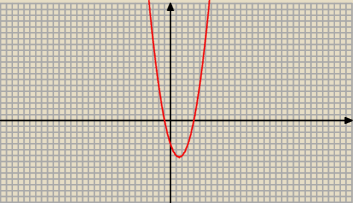
Janek191: t ∊ < t₁ ; t₂> i t > 0 więc t ∊ ( 0 ; t₂> = ( 0 ; 4> czyli 0 < 2^x ≤ 4 0 < x ≤ 2 ========

Maciej: Dziękuję