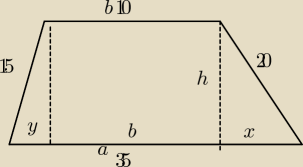
x+y+10=35 z czego wynika: x+y=25
Z twierdzenia Pitagorasa mamy dwa równania:
y2+h2=152
x2+h2=202
Otrzymujemy układ 3 równań z 3 niewiadomymi:
y2+h2=152
x2+h2=202
x+y=25
Z ostatniego równania wyliczamy x:
x=25−y,
a następnie podstawiamy do drugiego równania, otrzymując:
(25−y)2+h2=400,
następnie dodajemy stronami otrzymane równanie z równaniem pierwszym, otrzymując:
y=9,
mając wyliczone y możemy wyliczyć x podstawiając y do ostatniego równania (x=25−9), otrzymując:
x=16,
i na koniec wyliczmy wysokość podstawiając x albo y do odpowiedniego równania, na przykład y do
równania drugiego, otrzymując:
h2=400−256 (h=√144) z czego wynika, że wysokość h=12.
Mając wyliczoną wysokość trapezu możemy obliczyć jego pole:
| 1 | 1 | |||
P= | *(a+b)*h, (P=( | *(35+10)*12) | ||
| 2 | 2 |
Dziękuję Ci jeszcze raz!
