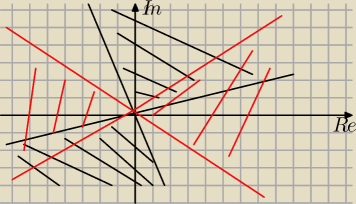
jerey: zostały mi jeszcze 2 przykłady z którymi mam problem. narysowac zbiory liczb zespolonych spełniająchych podane warunki; Im(z²)≥Re[(z⁻)²] podstawiając z=x+yi z⁻=x−yi dochodzę do: 2xy≥x²−y² graficznie wychodzą mi 2 przecinające sie linie w odpowiedzi mam półpłaszczyzny czarne jak na rysunku wyzej

	(1+i)z
2gi przykład: Im		≥0
	(1−i)z−

	2x2−2y2
usuwam sprzężenie i podstawiam z=x+yi, z−=x−yi dostaje :
	2(x2+y2)

w odp mam połpaszczyzny czerwone jak na rysunku wyzej pomoze ktos uporac się z tymi zadaniami?

Kris: Ok co do 1 przykladu to najlepiej to ze wzoru Moivre'a czyli Im(z²) ≥ Re[(z⁻)²] r²*sin2φ ≥ r²* cos2φ A co do drugiego to po przekształceniach wychodzi

2x2 − 2y2
	≥ 0
(x−y)2 + (y + x)2

co daje |x| ≥ |y|

Kris: Czyli w tym pierwszym sprawdzasz kiedy sin2φ ≥ cos2φ a w drugim cos musiales zle przekształcić

lwg: Niestety, nie idę po Ciebie.

jerey: dzieki Kris

Kris: A nie dobrze przekształciłeś tylko ja o 2 w nocy wyłączam myślenie