jerey: narysowac zbiory liczb zespolonych z spełniających podane warunki. Im(z⁶)<0 w ksiązce mam to rozpisane ze wzoru de Moivre'a Im[r⁶(cos6φ+isin6φ)]<0 ⇔ r⁶sin6φ<0 r>0 i sin6φ<0

	π		π		π		2π		11π
r>0 i φ ∊ (		,		) ∪ (		,		) ∪ .... (		,2π)
	6		3		2		3		6

nie ogarniam skąd te wartosci kątów, mogłby ktoś wytłumaczyc?

MQ: Z warunku sin(6φ)<0

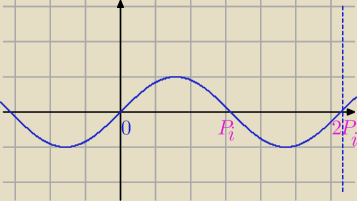
Mila: sin(6φ)<0⇔π+2kπ<(6φ)<2π+2kπ/:6

π		2kπ		2π		2kπ
	+		<φ<		+		⇔
6		6		6		6

Liczysz które przedziały są w (0,2π) k=0⇔

	π		π
φ∊(		,		)
	6		3

k=1

	π		2π
φ∊(		,		)
	2		3

licz dalej sam

razor:

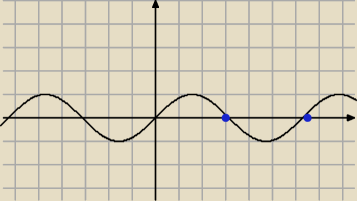
	π		kπ		π		kπ
sin6x < 0 → 6x ∊ (π+2kπ,2π+2kπ) → x ∊ (		+		,		+		), k ∊ Z
	6		3		3		3

wstawiając k = 0,1,2... otrzymasz przedział który podałeś

jerey: dziekuje wam, jesteście niezastąpieni .