Da się narysować wykres funkcji mając równanie y=1+log(x+1) ? Rafal: Da się narysować wykres funkcji mając równanie y=1+log(x+1) ?

razor: jest to wykres funkcji logx po przesunięciu o wektor [−1,1]

Rafal: Czyli? Z kąd wiesz o jaki ile trzeba ją przesunąć?

razor: Skąd wiem? 48

J : f(x) → [ a,b ] → f(x − a) + b

Rafal: Ok wektory już rozumiem ale w ciąż nie wiem jak wyznaczyć dowolny punkt na osi .

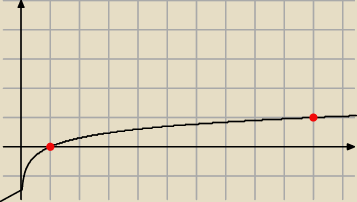
razor: logx = 0 → x = 1 logx = 1 → x = 10

Rafal: a nie popełniłeś błędu przy rysowaniu wykresu?

Mila: https://matematykaszkolna.pl/strona/2908.html

Rafal: Nie rozumiem jak to zrobić bo jak za x podstawiam −4 to nic nie wychodzi

J : a do czego podstawiasz − 4 ... ?

Rafal: zrobiłem tak y=logx −4=logx i właśnie nie wiem co dalej zrobić

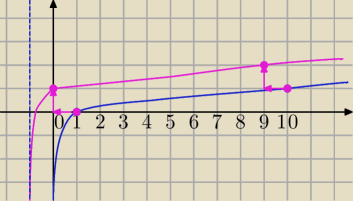
Mila: x+1>0⇔x>−1 Masz naszkicować wykres. Logarytm ma podstawę 10. Wybierasz taki argument, aby łatwo obliczyć logarytm y=log(x), funkcja rosnąca x=1 log(1)=0 bo 10⁰=1 log(10)=1 bo 10¹=10

	1
log(		)=−1
	10

Translacja o wektor [−1,1]⇒y=1+log(x+1)

Rafal: Jeszcze jedno putanie skąd wiadomo, że funkcja dąży do 0.

Mila: Gdzie dąży do zera?

Rafal: w sensie zaczyna się od 0 ale nie styka się z nim

Rafal: dąży do +∞

Rafal: rozumiem, że log(1)=0 ale dlaczego ten wykres zaczyna się −∞ ale ma granice 0 a nie po prostu od 0?

Mila: dla x→0₊ funkcjay= log(x)→−∞ Z definicji logarytmu.

	1
log		=log10−1000=−1000
	101000

	1
log		=log10−1000000=−1000000
	101000000

Rafal: ok juz rozumiem dziękuję

Mila: Poczytaj o funkcji logarytmicznej. https://matematykaszkolna.pl/strona/3417.html