granice kyrtap: Znajdź obie granice jednostronne (właściwe bądź niewłaściwe) we wskazanym punkcie:

	x−1
a) y =		w punkcie 1
	Ix−1I

o co tutaj chodzi? może ktoś na tym przykładzie wytłumaczyć

Martiminiano: Za chwilkę Ci napiszę jak ja to rozumiem.

Martiminiano: Definicja książkowa granica jednostronna właściwa: Dana jest funkcja y=f(x), której dziedziną D jest zbiór R albo przedział liczbowy, albo suma przedziałów. Mówimy, że funkcja f ma w punkcie x₀ granicę prawostronną (lewostronną) równą g wtedy i tylko wtedy, gdy dla dowolnego ciągu argumentów (x_n) o wyrazach większych (mniejszych) i zbieżnego do x₀ odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby g. Przy obliczaniu granic jednostronnych stosuje się poznane twierdzenia dotyczące działań na graniach funkcji. Podstawiasz wartość za x i liczysz, w tym przypadku granica będzie niewłaściwa, bo jak podstawiłbyś 1, to w mianowniku wyszłoby 0. Defincja książkowa granica jednostronna niewłaściwa: Definicja książkowa: Dana jest funkcja y=f(x), której dziedziną D jest zbiór R albo przedział liczbowy, albo suma przedziałów. Mówimy, że funkcja f ma w punkcie x₀ granicę niewłaściwą nieskończoność (minus nieskończoność) wtedy i tylko wtedy, gdy dla dowolnego ciągu argumentów (x_n) o wyrazach różnych od x₀ i zbieżnego do x₀ odpowiadający mu ciąg wartości funkcji jest rozbieżny do nieskończoności (minus nieskończoności). A teraz zadanie.

kyrtap: jestem ciekaw

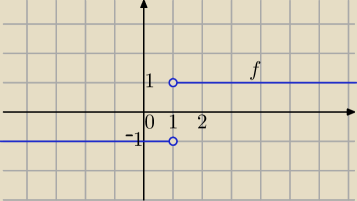
Martiminiano: Na początek zrobiłbym tak: Dla x≥1 f(x)=1

	x−1
Dla x<1 f(x)=
	1−x

lim_x→1⁺ f(x)=1

	x−1
limx→1−		=−∞
	1−x

Argumenty dążą do 1 z lewej strony na osi. Mianownik dąży do 0, wartości funkcji dla x→1⁻ są ujemne (w liczniku mamy 0⁻, a w mianowniku 0⁺, plus i minus daje minus)

kyrtap: przypadkiem z lewej strony granica − 1

Martiminiano: Więc w pierwszym przypadku jest granica właściwa, a w drugim niewłaściwa. Dodatkowo ważne twierdzenie, które przyda się przy wykazywaniu ciągłości funkcji: Granica lim_x→x0f(x) istnieje wtedy i tylko wtedy, gdy istnieją granice jednostronne lim_x→x0⁺ f(x) i lim_x→x0⁻ f(x) oraz lim_x→x0⁺ f(x)= lim_x→x0⁻ f(x) I kolejne trzy ważne rzeczy: Jeżeli funkcja y=f(x) ma w punkcie x₀ granicę jednostronną niewłaściwą, to prostą x=x₀ nazywamy asymptotą pionową wykresu funkcji Jeżeli lim_x→∞ f(x)=g, to prostą y=g nazywamy asymptotą poziomą wykresu funkcji w nieskończoności Jeżeli lim_x→−∞ f(x)=k, to prostą y=k nazywamy asymptotą poziomą wykresu funkcji w minus nieskończoności

Martiminiano: Moim zdaniem zrobiłem to dobrze, mam nadzieję, że nie sieję herezji . Może ktoś jeszcze odpowie.

Eta:

	x−1
dla x>1 f(x)=		=1
	x−1

	x−1
dla x<1 f(x)=		= −1
	−(x−1)

Kacper: Ale referaty

Martiminiano: Jednak źle A tyle się naprodukowałem

Martiminiano: Głupotę zrobiłem przy wartości bezwzględnej... Jak chcesz to mogę podać Ci kilka przykładów z podręcznika na granice jednostronne właściwe i niewłaściwe

Eta:

Eta:

Mila: A co chcesz Eto zobaczyć?

Eta: próbną

Mila:

Eta: Mila arkusze z próbnej !