nierownosci Hania =): BARDZO PROSZE O POMOC I WYJASNIENIE. Rozwiaz nierownosc: 3+2x −−−−−−− ≥ 0 (2x +1)(x−3) x² − 3x+2 −−−−−−−−−−−−−− < 0 x² − 9

Nikka: coś zapis nie ten tego i nie wiadomo o co chodzi...

Hania =): jak to nie wiadomo? nierownosc w ulamku i tyle.

Nikka: tylko, że tych ułamków nie mogę odczytać, nie wiadomo co jest w liczniku a co w mianowniku

Hania =): u gory to co jest wyzej jest w liczniku a to co na dole nizej w mianowniku to sa dwa przyklady. prosze o pomoc bo mi to nie chce wyjsc.!:((

Nikka: wiem co to jest licznik i mianownik... Twój zapis wygląda tak 3+2x −−−−−−−−−−−−−−−−−−−−−−−−−−−≥0, (2x+1)(x−3) x²≥−3x+2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−<0 x²−9 jak mam z tego odczytać co powinno być w liczniku, a co w mianowniku?!

Hania =): naprawde tak to wyglada? u mnie wyglada zupelnie inaczej, dlatego przepraszam 3+2x − licznik (2x +1)(x−3) − mianownik x2 − 3x+2 licznik x2 − 9 mianownik

Nikka:

	3+2x		−3x+2
czyli		≥ 0 i		<0
	(2x−1)(x−3)		x2−9

Hania =): x² − 3x+2 − licznik drugiego

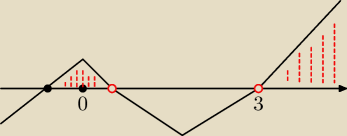
Nikka: no tak, nie zauważyłam Przykład 1. D: 2x−1≠0 i x−3≠0

	1
x≠		i x≠3
	2

	1
D=R\{		, 3}
	2

(po lewej stronie mamy funkcję w postaci ułamka, mianownik nie może być równy zero, czyli musi być różny od zera) Mnożymy obie strony nierówności przez [(2x−1)(x−3)]² (w ten sposób monożymy przez liczbę dodatnią i nie zmieniamy znaku nierówności) i otrzymujemy: (3+2x)(2x−1)(x−3) ≥ 0

	3		1
(x= −		, x=		, x=3)
	2		2

Tu wstawiamy rysunek i odczytujemy :

	3		1
x∊<−		,		)∪(3,∞)
	2		2

Hania =): a drugi przyklad?;>

Nikka: a drugi spróbuj sama

Nikka: zacznij od dziedziny, a ja czekam co Ci będzie wychodzić i pomogę w razie potrzeby...

Hania =): ehh no ok tylko mi powiedz czy mianownik rozbic ze wzrou skroconego mnozenia?

Hania =): ehh no ok tylko mi powiedz czy mianownik rozbic ze wzrou skroconego mnozenia?

Nikka: dokładnie − brawo D: x²−9≠0 i co dalej?

Hania =): x rozne od 3 i −3?

Hania =): x rozne od 3 i −3?

Nikka: dokładnie D=R\{−3,3} dalej...

Hania =): obustronnie mnozymy przez x² − 9 d kwadratu i powstaje: (x²−3x+2)(x²−9) i obliczam delte i miejsca zerowe

Nikka: bardzo dobrze dla pierwszego nawiasu policz Δ i pierwiastki, drugi wystarczy rozpisać ze wzoru skróconego mnożenia tak jak to zrobiłaś licząc dziedzinę, z takiej postaci można odczytać pierwiastki czyli to 3, −3

Hania =): tak i moje pytanie brzmi czy na wykresie brac pod uwage 3 i −3 skoro x ma byc rozne od 3 i −3

Nikka: na wykresie w −3 i 3 będą kółeczka otwarte bo −3 i 3 musieliśmy wyrzucić z dziedziny jakie pierwiastki otrzymałaś z pierwszego nawiasu?

Hania =): 1 i 2?;> aha to czyli juz mniej wiecej rozumiem dziekuje bardzo

Nikka: 1 i 2 też będą otwarte w odpowiedzi bo mamy jako znak nierówności <

Nikka: jaka odpowiedz otrzymałaś ?

Hania =): x nalezy −3,1 i 2,3 wszystko otwarte;>

Nikka: brawo

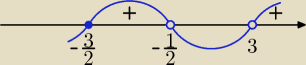
Bogdan: Czas najwyższy poprawnie poprowadzić rozwiązanie tych nierówności:

3 + 2x		3   2(x + )   2
	≥ 0 ⇒		≥ 0
(2x + 1)(x − 3)		1   2(x + )(x − 3)   2

	1
założenie: x ≠ −		i x ≠ 3
	2

3   (x + )   2		3		1
	≥ 0 ⇔ (x +		)(x +		)(x − 3) ≥ 0
1   (x + )(x − 3)   2		2		2

	3		1
Odp.: x∊<−		, −		)∪(3, +∞)
	2		2

Nikka: ups, zrobiłam błąd w obliczeniach ( a tak się starałam) czy możesz Bogdanie sprawdzić b)

Bogdan:

x2 − 3x + 2
	< 0, założenie: x2 − 9 ≠ 0 ⇒ x ≠ − 3 i x ≠ 3.
x2 − 9

(x − 2)(x − 1)
	< 0 ⇔ (x − 2)(x − 1)(x − 3)(x + 3) < 0
(x − 3)(x + 3)

x ∊ .....

Nikka: x∊(−3,1) ∪ (2,3)

Bogdan:

Hania =): dziekuuuje Wam