| √6 | ||
dwusieczną kąta ACB w punkcie E. Wykaż, że długość odcinka DE jest równa | ||
| 2 |
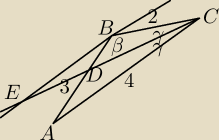 β − kąt przy wierzchołku B
Tw. cosinusów:
16=4+9 − 12cosβ
cosβ = −1/4 , więc △ABC rozwartokątny
z: rys.
t: |DE| = √6/2
d: tw. o dwusiecznej:
|BC|/|BD| = |AC|/|AD| ∧ |AD| = 3 − |BD|
po wykonaniu obliczeń wychodzi |BD| = 1; |AD| = 2
tw. cosinusów w △BDC:
|CD|2 = 5 − 4cosβ = 6
|CD| = √6 ,bo |CD|>0
Tutaj się zatrzymałem
β − kąt przy wierzchołku B
Tw. cosinusów:
16=4+9 − 12cosβ
cosβ = −1/4 , więc △ABC rozwartokątny
z: rys.
t: |DE| = √6/2
d: tw. o dwusiecznej:
|BC|/|BD| = |AC|/|AD| ∧ |AD| = 3 − |BD|
po wykonaniu obliczeń wychodzi |BD| = 1; |AD| = 2
tw. cosinusów w △BDC:
|CD|2 = 5 − 4cosβ = 6
|CD| = √6 ,bo |CD|>0
Tutaj się zatrzymałem